2022年浙教版数学八年级上学期第3章 一元一次不等式 单元检测
试卷更新日期:2022-07-24 类型:单元试卷
一、单选题(每小题3分,共30分)
-
1. 在数轴上表示不等式的解集正确的是A、
 B、
B、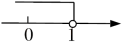 C、
C、 D、
D、 2. 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
2. 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( ) A、 B、 C、 D、3. 若a>b,则下列各式正确的是( )A、a﹣b<0 B、3﹣a<3﹣b C、|a|>|b| D、4. 已知关于的不等式的解集为 , 则的取值范围是A、 B、 C、 D、5. 下列说法正确的是( )A、若x>3,则x>4 B、若x>3,则x<4 C、若x>4,则x>3 D、若x>4,则x<36. 已知x=2不是关于x的不等式2x-m>4的整数解,x=3是关于x的不等式2x-m>4的一个整数解,则m的取值范围为( )A、0<m<2 B、0≤m<2 C、0<m≤2 D、0≤m≤27. 不等式组 的解集在数轴上可表示为( )A、
A、 B、 C、 D、3. 若a>b,则下列各式正确的是( )A、a﹣b<0 B、3﹣a<3﹣b C、|a|>|b| D、4. 已知关于的不等式的解集为 , 则的取值范围是A、 B、 C、 D、5. 下列说法正确的是( )A、若x>3,则x>4 B、若x>3,则x<4 C、若x>4,则x>3 D、若x>4,则x<36. 已知x=2不是关于x的不等式2x-m>4的整数解,x=3是关于x的不等式2x-m>4的一个整数解,则m的取值范围为( )A、0<m<2 B、0≤m<2 C、0<m≤2 D、0≤m≤27. 不等式组 的解集在数轴上可表示为( )A、 B、
B、 C、
C、 D、
D、 8. 已知关于x的不等式组 只有四个整数解,则实数a的取值范围( )A、﹣3≤a<﹣2 B、﹣3≤a≤﹣2 C、﹣3<a≤﹣2 D、﹣3<a<﹣29. 关于x,y的方程组 ,已知-4<a<0,则x+y的取值范围为( )A、0<x+y<2 B、-1<x+y<3 C、0<x+y<4 D、-1<x+y<210. 随看科技的进步,我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车,可又不想静静地等在A站.他从A站往B站走了一段路,拿出手机查看了公交车到站情况,发现他与公交车的距离为720m(如图),此时有两种选择:
8. 已知关于x的不等式组 只有四个整数解,则实数a的取值范围( )A、﹣3≤a<﹣2 B、﹣3≤a≤﹣2 C、﹣3<a≤﹣2 D、﹣3<a<﹣29. 关于x,y的方程组 ,已知-4<a<0,则x+y的取值范围为( )A、0<x+y<2 B、-1<x+y<3 C、0<x+y<4 D、-1<x+y<210. 随看科技的进步,我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车,可又不想静静地等在A站.他从A站往B站走了一段路,拿出手机查看了公交车到站情况,发现他与公交车的距离为720m(如图),此时有两种选择:
( 1 )与公交车相向而行,到A公交站去乘车;(2)与公交车同向而行,到B公交站去乘车.假设小明的速度是公交车速度的 ,若要保证小明不会错过这辆公交车,则A,B两公交站之间的距离最大为( )
A、240m B、300m C、320m D、360m二、填空题(每小题4分,共24分)
-
11. 不等式的解为.12. 不等式组 的整数解是 .13. 如果关于x的不等式组 的整数解只有1,2,3,那么a的取值范围是 , b的取值范围是.14. 已知关于 的不等式组 无解,则 的取值范围是 .15. 不等式 的最小负整数解.16. 一张试卷共25道题,做对一道题得4分,做错或不做倒扣1分,做完试卷得分不少于70分,则她至少做对了 道题.
三、解答题(共8题,共66分)
-
17. 解不等式组:并把解集在数轴上表示出来.18. 解不等式组 ,并写出所有整数解.(不画数轴)19. 一工厂要将100吨货物运往外地,计划租用某运输公司甲、乙两种型号的汽车共6辆一次将货物全部运输.已知每辆甲型汽车最多能装该种货物16吨,租金800元,每辆乙型汽车最多能装该种货物18吨,租金850元,若此工厂计划此次租车费用不超过5000元,通过计算求出该公司共有几种租车方案?请你设计出来,并求出最低的租车费用.20. 解不等式组 , 并把解集表示在数轴上.
 21. 已知.(1)、比较与的大小,并说明理由.(2)、若 , 求a的取值范围.22. 按照学校均衡发展的配备标准,某校计划采购 、 两种型号电脑.已知每台 种型号电脑价格比每台 种型号电脑价格多840元,且用25200元买 种型号电脑的台数与用21000元买 种型号电脑的台数一样多.(1)、求 、 两种型号电脑每台价格各为多少元?(2)、学校预计用不多于9万元的资金购进这两种电脑共20台,则最多可购买 种型号电脑多少台?23. 某社区拟建甲,乙两类摊位以激活“地摊经济”,1个甲类摊位和2个乙类摊位共占地面积14平方米,2个甲类摊位和3个乙类摊位共占地面积24平方米.(1)、求每个甲,乙类摊位占地面积各为多少平方米?(2)、该社区拟建甲,乙两类摊位共100个,且乙类摊位的数量不多于甲类摊位数量的3倍,求甲类摊位至少建多少个?24. 为拓展学生视野,丰富学生的社会实践经验。某校计划组织师生共300人前往江山绿然滕农场开展研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30 人,学校决定调整租车方案.在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
21. 已知.(1)、比较与的大小,并说明理由.(2)、若 , 求a的取值范围.22. 按照学校均衡发展的配备标准,某校计划采购 、 两种型号电脑.已知每台 种型号电脑价格比每台 种型号电脑价格多840元,且用25200元买 种型号电脑的台数与用21000元买 种型号电脑的台数一样多.(1)、求 、 两种型号电脑每台价格各为多少元?(2)、学校预计用不多于9万元的资金购进这两种电脑共20台,则最多可购买 种型号电脑多少台?23. 某社区拟建甲,乙两类摊位以激活“地摊经济”,1个甲类摊位和2个乙类摊位共占地面积14平方米,2个甲类摊位和3个乙类摊位共占地面积24平方米.(1)、求每个甲,乙类摊位占地面积各为多少平方米?(2)、该社区拟建甲,乙两类摊位共100个,且乙类摊位的数量不多于甲类摊位数量的3倍,求甲类摊位至少建多少个?24. 为拓展学生视野,丰富学生的社会实践经验。某校计划组织师生共300人前往江山绿然滕农场开展研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30 人,学校决定调整租车方案.在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.