2022-2023学年浙教版数学八年级上册3.3 一元一次不等式 同步练习

试卷更新日期：2022-07-24 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 一个不等式的解集在数轴上表示如图所示，则这个不等式可能是（   ）

    A、x>−1 B、x≥−1 C、x<−1 D、x≤−1

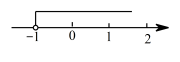    查看试题解析

  • 2. 某商店为了促销一种定价为3元的商品，采取下列方式优惠销售：若一次性购买不超过5件，按原价付款；若一次性购买5件以上，超过部分按原价八折付款.如果小明有30元钱，那么他最多可以购买该商品（　　）
    A、9件 B、10件 C、11件 D、12件

    查看试题解析

  • 3. 随着科技的进步，在很多城市都可以通过手机APP实时查看公交车到站情况.小聪同学想乘公交车，他走到A、B两站之间的C处，拿出手机查看了公交车到站情况，发现他与公交车的距离为700m（如图），此时他有两种选择：
    ①与公交车相向而行，到A公交站去乘车；
    ②与公交车同向而行，到B公交站去乘车.
    假设公交车的速度是小聪速度的6倍，小聪无论选择哪站乘坐都不会错过这辆公交车，则A，B两公交站之间的距离最大为（   ）

     
    A、240m B、260m C、280m D、300m

    查看试题解析

  • 4. 不等式 x3−x−12≥1 的最大整数解是（   ）
    A、0 B、−1 C、−2 D、−3

    查看试题解析

  • 5. 不等式 x−1<0 的解在数轴上表示为（   ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 某次知识竞赛共20道题，每一题答对得10分，不答得0分，答错扣5分，小聪有一道题没答，竞赛成绩超过90分.设他答对了x道题，则根据题意可列出不等式为（  ）
    A、10x﹣5（19﹣x）≥90 B、10x﹣5（19﹣x）＞90 C、10x﹣（19﹣x）≥90 D、10x﹣（19﹣x）＞90

    查看试题解析

  • 7. x=1是不等式x−b<0的一个解，则b的值不可能是（   ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 8. 某次知识竞赛一共有20道题，答对一题得5分，不答得0分，答错扣2分.小聪有1道题没答，竞赛成绩超过80分，则小聪至少答对的题数是（ ）
    A、15 B、16 C、17 D、18

    查看试题解析

  • 9. 不等式3x+4 ≥ 1的解集是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 10. 若关于x的不等式mx﹣n＞0的解集是x＜ 15 ，则关于x的不等式（m+n）x＞n﹣m的解集是（　  　）
    A、x＜﹣ 23 B、x＞﹣ 23 C、x＜ 23 D、x＞ 23

    查看试题解析

二、填空题

  • 11. 不等式 3x−5>1 的最小整数解是.

    查看试题解析

  • 12. 不等式2x﹣1≤6的非负整数解有个．

    查看试题解析

  • 13. 某产品进价为每件200元，商店标价为每件300元.现商店准备将这批服装打折出售，但要保证毛利润不低于5%，则商店最低可按折出售.

    查看试题解析

  • 14. 某种家用电器的进价为每件800元，以每件1200元的标价出售，由于电器积压，商店准备打折销售，但要保证利润率不低于5%，则最低可按标价的折出售.

    查看试题解析

  • 15. 一次知识竞赛一共有26道题，答对一题得4分，不答得0分，答错一题扣2分，小明有1道题没答，竞赛成绩不少于88分，则小明至少答对题.

    查看试题解析

  • 16. 不等式3x−1≤2x的解集是 ．

    查看试题解析

三、解答题

  • 17. 解不等式3(x-1)≤9，并把解在数轴上表示出来.

    查看试题解析

  • 18. 某业主贷款3.3万元购进一台机器，生产某种产品．已知产品的成本是每个3元，售价是每个5元，应付的税款和其它费用是售价的10%．若每个月能生产、销售6000个产品，问至少几个月后能赚回这台机器的贷款？（用列不等式的方法解决）．

    查看试题解析

  • 19. 某业主贷款88000元购进一台机器，生产某种产品，已知产品的成本是每个5元，售价是每个8元，应付的税款和其他费用是售价的10%，若每个月能生产、销售8000个产品，问至少几个月后能赚回这台机器贷款？（用列不等式的方法解决）

    查看试题解析

  • 20. 解不等式 x2<1−x−34 ，把它的解在数轴上表示出来，并写出该不等式的自然数解.

    查看试题解析

  • 21. 新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控.某呼吸机厂接到生产600台呼吸机的任务，以每天比原来多生产50台呼吸机的速度进行生产，结果所用时间与原来生产450台呼吸机所用时间相同.
    (1)、求该厂现在每天生产多少台呼吸机?
    (2)、完成这批任务后，该厂又接到在10天内至少生产2400台呼吸机的任务，问该厂每天还应该至少比现在多生产多少台呼吸机才能完成任务?

    查看试题解析

  • 22. 城市因文明而美丽，市民因礼仪而优雅.在长沙市创建全国文明典范城市的过程中，太阳山社区为了巩固垃圾分类的成果，营造干净整洁的生活氛围，创建和谐文明的社区环境、准备购买A、B两种分类垃圾桶，通过市场调研得知：A种垃圾桶每组的单价比B种垃圾桶每组的单价少150元，且用18000元购买A种垃圾桶的组数是用13500元购买B种垃圾桶的组数的2倍.
    (1)、求A、B两种垃圾桶每组的单价分别是多少元；
    (2)、该社区计划用不超过8000元的资金购买A、B两种垃圾桶共20组，则最多可以购买B种垃圾桶多少组？

    查看试题解析

  • 23. 今年4月23日是第26个世界读书日.八（1）班举办了“让读书成为习惯，让书香飘满校园”主题活动.准备订购一批新的图书鲁迅文集（套）和四大名著（套）.
    (1)、采购员从市场上了解到四大名著（套）的单价比鲁迅文集（套）的单价的贵25元.花费1000元购买鲁迅文集（套）的数量与花费1500元购买鲁迅文集（套）的数量相同.求鲁迅文集（套）和四大名著（套）的单价各是多少元？
    (2)、若购买鲁迅文集和四大名著共10套（两类图书都要买），总费用不超过570元，问该班有哪几种购买方案？

    查看试题解析

  • 24. 2020年武汉封城期间，某社区模范党员服务队为了给市民配送生活物资，准备从批发市场购进甲、乙、丙三种物资，已知每千克乙物资的进价比每千克甲物资的进价多5元，每千克丙物资的进价是每千克甲物资进价的3倍，用270元购进丙物资的重量是用60元购进乙物资的重量的3倍.
    (1)、求甲、乙、丙三种物资的购进价格分别是多少元？
    (2)、该社区购进甲、乙、丙三种物资共400kg，其中乙物资的重量是丙物资重量的2倍，且甲、丙两种物资重量之和不超过乙物资重量的3倍，则丙物资至少购进多少千克使总花费最少？总花费最少是多少元？

    查看试题解析