2022-2023学年浙教版数学八年级上册3.2 不等式的基本性质同步练习

试卷更新日期：2022-07-24 类型：同步测试

进入出卷网下载

一、单选题

1. 已知x≤y下列式子中成立的是（）

A、 $x + 1 ⩽ y + 1$ B、 $\frac{x}{c} ⩽ \frac{y}{c}$ C、 $x + 1 ⩽ y - 1$ D、 $x c ⩽ y c$

查看试题解析
2. 已知a＜b，下列式子正确的是（）

A、a+3＞b+3 B、a﹣3＜b﹣3 C、﹣3a＜﹣3b D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
3. 如图，若点A表示数为 $x + 1$ .则（）

A、 $- 3 < x < - 2$ B、 $- 2 < x < - 1$ C、 $- 1 < x < 0$ D、 $0 < x < 1$

查看试题解析
4. 已知 a，b都是实数，且a<b，则下列不等式的变形正确的是（ )

A、a-1>b-1 B、-a+2<-b+2 C、3a<3b D、 $\frac{a}{2} > \frac{b}{3}$

查看试题解析
5. 估计 $2 \sqrt{11} + 1$ 的值在（）

A、5到6之间 B、6到7之间 C、7到8之间 D、8到9之间

查看试题解析
6. 若x+2022>y+2022，则（）

A、x+2<y+2 B、x－2<y－2 C、－2x<－2y D、2x<2y

查看试题解析
7. 若不等式（a+1）x>2的解集为x< $\frac{2}{a + 1}$ ，则a的取值范围是（）

A、a<1 B、a<-1 C、a>1 D、a>-1

查看试题解析
8. 下列不等式变形中，一定正确的是（）

A、若ac＞bc，则a＞b B、若a＞b，则ac²＞bc² C、若ac²＞bc² ，则a＞b D、若a＞0，b＞0，且 $\frac{1}{a} > \frac{1}{b}$ ，则a＞b

查看试题解析
9. 若a＞b，下列不等式不一定成立的是（）

A、a﹣2021＞b﹣2021 B、﹣2021a＜﹣2021b C、 $\frac{a}{c} > \frac{b}{c}$ D、a+c＞b+c

查看试题解析
10. 如果 $m < n < 0$ ，那么下列结论中错误的是（）．

A、 $m - 9 < n - 9$ B、 $- m > - n$ C、 $m - n > 0$ D、 $\frac{m}{n} > 1$

查看试题解析

二、填空题

11. 若 $x > y$ ，则 $3 - 5 x$ $3 - 5 y$ （填“＞”或“＝”或“＜”）.

查看试题解析
12. 比较大小，用“ $>$ ”或“ $<$ ”填空：

(1)、若 $x < y$ ，且 $(a - b) x > (a - b) y$ ，则 $a$ $b$ .

(2)、若 $a$ ， $b$ 为实数，则 $4 + 3 a^{2} - 2 b + b^{2}$ $3 a^{2} - 2 b + 1$ .

查看试题解析
13. 如果不等式（b+1）x＜b+1的解集是x＞1，那么b的范围是 .

查看试题解析
14. 已知 $a b = 2$ ， $- 3 \leq b \leq - 1$ ，则a的取值范围是.

查看试题解析
15. 下列命题中：
①若 $a > b$ ，则 $a - b < 0$ ；

②若 $a < 0$ ，则 $b - a > b$ ；

③若 $a > b$ ，则 $b c^{2} < a c^{2} (c \neq 0)$ ；

④若 $a x > - a$ ，则 $x > - 1$ ．

正确的有．（只填写正确命题的序号）

查看试题解析
16. 定义：用符号 $[m]$ 表示一个实数 $m$ 的整数部分，例如： $[1.5] = 1$ ， $[0.25] = 0$ ， $[π] = 3$ .按此定义，计算 $[8 - \sqrt{19}] =$ .

查看试题解析

三、解答题

17. 某数学兴趣小组在学习“不等式的性质”时，有两名同学的对话如下：

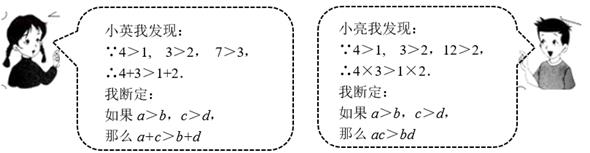
你认为小英和小亮的结论正确吗？如果正确，请说明理由；如果不正确，请举出一个反例。

查看试题解析
18. 已知a＜0，-1＜b＜0，试比较a、ab、ab²的大小．

查看试题解析
19. 说出下列不等式的变形是根据不等式的哪一条性质：

(1)、由3＋x≤5，得x≤2；

(2)、由3x≥2x－4，得x≥－4.

查看试题解析
20. 依据不等式的性质，把下列不等式化成x>a或x<a的形式：

(1)、x+3<5

(2)、x- $\frac{4}{5}$ > $\frac{1}{5}$

查看试题解析

四、综合题

21. 若x<y，试比较下列各对式子的值的大小，并说明依据：

(1)、-2x与-2y；

(2)、3-2x与3-2y．

查看试题解析
22. 现有不等式的两个性质：①在不等式的两边都加上(或减去)同一个数(或整式)，不等号的方向不变.②在不等式的两边都乘同一个数(或整式)，乘的数(或整式)为正时不等号的方向不变，乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题：

(1)、利用性质①比较2a 与a 的大小(a≠0).

(2)、利用性质②比较2a 与a 的大小(a≠0).

查看试题解析
23. 两个非负实数a和b满足a+2b=3，且c=3a+2b
求：

(1)、求a的取值范围；

(2)、请用含a的代数式表示c，并求c的取值范围.

查看试题解析
24. 阅读理解：我们知道，比较两数（式）大小有很多方法，“作差法”是常用的方法之一，其原理是不等式（或等式）的性质：若 $a - b > 0$ ，则 $a > b$ ；若 $a - b = 0$ ，则 $a = b$ ；若 $a - b < 0$ ，则 $a < b$ .
例：已知 $A = x^{2} + 2 x y$ ， $B = 4 x y - y^{2}$ ，其中 $x \neq y$ ，求证： $A > B$ .

证明： $A - B = (x^{2} + 2 x y) - (4 x y - y^{2}) = x^{2} + 2 x y - 4 x y + y^{2}$ $= x^{2} - 2 x y + y^{2} = {(x - y)}^{2}$ .

∵ $x \neq y$ ，∴ ${(x - y)}^{2} > 0$ ，∴ $A > B$ .

(1)、操作感知：比较大小：
①若 $a < b < 0$ ，则 $a^{3}$ $a b^{2}$ ；

② $m^{2} + 16$ $8 m$ .

(2)、类比探究：已知 $M = 2016 \times 2019$ ， $N = 2017 \times 2018$ ，试运用上述方法比较 $M$ 、 $N$ 的大小，并说明理由.

(3)、应用拓展：已知 $P (m ， m - 4)$ ， $Q (m ， m^{2} + 3 m)$ 为平面直角坐标系中的两点，小明认为，无论 $m$ 取何值，点 $Q$ 始终在点 $P$ 的上方，小明的猜想对吗？为什么？

查看试题解析

2022-2023学年浙教版数学八年级上册3.2 不等式的基本性质 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

2022-2023学年浙教版数学八年级上册3.2 不等式的基本性质同步练习