2022-2023初数北师大版八年级上册4.4一次函数的应用 同步练习
试卷更新日期:2022-07-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 一次函数的图象与y轴交点是( )A、(﹣1,0) B、(2,0) C、(0,1) D、(0,﹣1)2. 在探究“水沸腾时温度变化特点”的实验中,下表记录了实验中温度和时间变化的数据.
时间/分钟
0
5
10
15
20
25
温度/℃
10
25
40
55
70
85
若温度的变化是均匀的,则18分钟时的温度是( )
A、62℃ B、64℃ C、66℃ D、68℃3. 巴中某快递公司每天上午7:00﹣8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为( )①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为8件;
③8:00时,甲仓库内快件数为400件;
④7:20时,两仓库快递件数相同.
 A、1个 B、2个 C、3个 D、4个4. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( )
A、1个 B、2个 C、3个 D、4个4. 如图①是某公共汽车线路收支差额y(票价总收入减去运营成本)与乘客量x的函数图象,目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会,乘客代表认为:公交公司应降低运营成本,实现扭亏;公交公司认为:运营成本难以下降,提高票价才能扭亏;根据这两种意见,把图①分别改画成图②和图③,则下列判断不合理的是( ) A、图①中点A的实际意义是公交公司运营前期投入成本为1万元 B、图②能反映公交公司意见 C、图③能反映乘客意见 D、图②中当乘客量为1.5万时公交公司收支平衡5. 某品牌鞋子的长度ycm与鞋子的码数x之间满足一次函数关系.若23码鞋子的长度为16.5cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )A、23cm B、24cm C、25cm D、26cm6. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( )
A、图①中点A的实际意义是公交公司运营前期投入成本为1万元 B、图②能反映公交公司意见 C、图③能反映乘客意见 D、图②中当乘客量为1.5万时公交公司收支平衡5. 某品牌鞋子的长度ycm与鞋子的码数x之间满足一次函数关系.若23码鞋子的长度为16.5cm,44码鞋子的长度为27cm,则38码鞋子的长度为( )A、23cm B、24cm C、25cm D、26cm6. 14:00时,时钟中时针与分针的位置如图所示(分针在射线OA上),设经过xmin(0≤x≤30),时针、分针与射线OA所成角的度数分别为y1°、y2°,则y1、y2与x之间的函数关系图是 ( ) A、
A、 B、
B、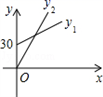 C、
C、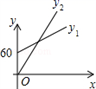 D、
D、 7. 如图所示直线反映了某公司产品的销售成本和销售收入与销售量之间的关系,则下列说法错误的是( )
7. 如图所示直线反映了某公司产品的销售成本和销售收入与销售量之间的关系,则下列说法错误的是( ) A、直线l1反映了该公司产品的销售收入与销售量之间的关系 B、未开始销售时,该公司为销售所花的成本为2000元 C、当销售量大于 4吨时,该公司赢利 D、每销售1吨产品,销售收入为 500 元8. 一蓄水池中有水 , 打开排水阀门开始放水后水池的水量与放水时间有如下关系:
A、直线l1反映了该公司产品的销售收入与销售量之间的关系 B、未开始销售时,该公司为销售所花的成本为2000元 C、当销售量大于 4吨时,该公司赢利 D、每销售1吨产品,销售收入为 500 元8. 一蓄水池中有水 , 打开排水阀门开始放水后水池的水量与放水时间有如下关系:放水时间/分
1
2
3
4
…
水池中水量/
48
46
44
42
…
下列说法错误的是( )
A、蓄水池每分钟放水 B、放水18分钟后,水池中水量为 C、蓄水池一共可以放水25分钟 D、放水12分钟后,水池中水量为9. 甲、乙两人分别从笔直道路上的A、B两地出发相向匀速而行,已知甲比乙先出发5分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟;②乙的速度是90米/分钟;③甲出发18分钟时,两人在C地相遇;④乙到达A地时,甲与A地相距460米,其中正确的说法有( ) A、①② B、①②③ C、①②④ D、①②③④10. 港口 依次在同一条直线上,甲、乙两艘船同时分别从 两港出发,匀速驶向 港,甲、乙两船与 港的距离 (海里)与行驶时间 (小时)之间的函数关系如图所示,则下列说法正确的有( )
A、①② B、①②③ C、①②④ D、①②③④10. 港口 依次在同一条直线上,甲、乙两艘船同时分别从 两港出发,匀速驶向 港,甲、乙两船与 港的距离 (海里)与行驶时间 (小时)之间的函数关系如图所示,则下列说法正确的有( )① 两港之间的距离为60海里
②甲、乙两船在途中只相遇了一次
③甲船平均速度比乙船平均速度快30海里/时
④甲船到达 港时,乙船还需要一个小时才到达 港
⑤点 的坐标为
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 某手工作坊生产并销售某种食品,假设销售量与产量相等,如图中的线段AB、OC分别表示每天生产成本(单位:元)、收入(单位:元)与产量x(单位:千克)之间的函数关系.若该手工作坊某一天既不盈利也不亏损,则这天的产量是千克.
 12. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中 、 分别表示去年、今年水费y(元)与用水量x( )之间的关系.小雨家去年用水量为150 ,若今年用水量与去年相同,水费将比去年多元.
12. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中 、 分别表示去年、今年水费y(元)与用水量x( )之间的关系.小雨家去年用水量为150 ,若今年用水量与去年相同,水费将比去年多元. 13. 已知直线 , 则它与x轴的交点坐标为 , 与坐标轴围成的三角形面积为.14. 一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为元.
13. 已知直线 , 则它与x轴的交点坐标为 , 与坐标轴围成的三角形面积为.14. 一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为元.型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
15. 声音在空气中的传播速度 与温度 的关系如表:温度(℃)
0
5
10
15
20
速度
331
336
341
346
351
若声音在空气中的传播速度 是温度 的一次函数;当 时,声音的传播速度为 .
16. 一条笔直的公路上依次有A,B,C三地,甲,乙两人同时从A地出发,甲先使用共享单车,经过B地到达停车点C地后再步行返回B地,此时直接步行的乙也恰好到达B地.已知两人步行速度相同,两人离起点A的距离y(米)关于时间x(分)的函数关系如图,则 .
三、解答题(共8题,共52分)
-
17. 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如下图中的一次函数 的图象与x轴、y轴分别相交于点E、F , 则△OEF为此函数的坐标三角形,求此坐标三角形的三条边长.
 18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围.
18. 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为35m,求鸡场的长y (m)与宽x (m)的函数关系式,并求自变量的取值范围. 19. 为提醒人们节约用水,及时修好漏水的水龙头,小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升。
19. 为提醒人们节约用水,及时修好漏水的水龙头,小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升。时间t(秒)
10
20
30
40
50
60
70
量筒内水量v(毫升)
4
6
8
10
12
14
16
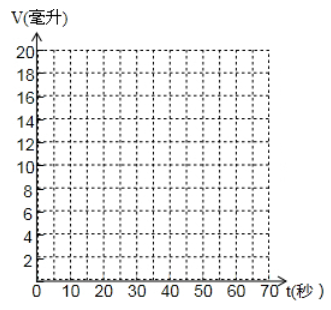 (1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:
(1)、在图1的平面直角坐标系中,以(t;v)为坐标描出上表中数据对应的点;(2)、用光滑的曲线连接各点,并写出你猜测的ⅴ与t的函数关系式。(3)、解决问题:①小明同学所用量筒开始实验前原有存水毫升;
②如果小明同学继续实验,当量筒中的水刚好盛满时所需时间是秒;
③按此漏水速度,半小时会漏水毫升。
20. 小聪和小慧去某风景区游览,约好在观景点见面.小聪步行先从景区入口处出发,中途休息片刻后继续以原速度前行,此时小慧乘观光车从景区入口处出发,他们沿相同路线先后到达观景点,如图,l1 , l2分别表示小聪与小慧离景区入口的路程y(千米)与时间x(分)之间的关系,根据图象解决下列问题: (1)、小聪步行的速度是(千米/分),中途休息分钟.(2)、求小慧离景区入口的路程y(千米)关于时间x(分)函数表达式.(3)、小慧比小聪早几分钟到达观景点?请说明理由.21. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠病毒疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务.乙地80天完成接种任务.在某段时间内,甲、乙两地的接种人数y(万人)与接种时间x(天)间的关系如图所示.
(1)、小聪步行的速度是(千米/分),中途休息分钟.(2)、求小慧离景区入口的路程y(千米)关于时间x(分)函数表达式.(3)、小慧比小聪早几分钟到达观景点?请说明理由.21. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠病毒疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务.乙地80天完成接种任务.在某段时间内,甲、乙两地的接种人数y(万人)与接种时间x(天)间的关系如图所示. (1)、乙地每天接种的人数为万人,a的值为;(2)、当甲地接种速度放缓后,求y与x之间的函数表达式;(3)、当甲地接种速度放缓后,完成接种任务之前,何时与乙地接种人数相同?相同人数是多少?22. 如图①,在一条笔直的公路上依次有A、B、C三地.一辆慢车从A地出发,沿公路匀速驶向C地.2小时后,一辆快车从C地出发,以每小时60千米的速度沿公路驶向B地,到达B地后停止.慢车、快车离B地的距离 、 与慢车行驶时间 之间的函数关系如图②所示.
(1)、乙地每天接种的人数为万人,a的值为;(2)、当甲地接种速度放缓后,求y与x之间的函数表达式;(3)、当甲地接种速度放缓后,完成接种任务之前,何时与乙地接种人数相同?相同人数是多少?22. 如图①,在一条笔直的公路上依次有A、B、C三地.一辆慢车从A地出发,沿公路匀速驶向C地.2小时后,一辆快车从C地出发,以每小时60千米的速度沿公路驶向B地,到达B地后停止.慢车、快车离B地的距离 、 与慢车行驶时间 之间的函数关系如图②所示. (1)、A、C两地之间的距离是km,慢车的速度是km/h;(2)、求点P的坐标,并解释点P的实际意义.(3)、画出两车之间的距离 与慢车行驶时间 之间的函数图象.
(1)、A、C两地之间的距离是km,慢车的速度是km/h;(2)、求点P的坐标,并解释点P的实际意义.(3)、画出两车之间的距离 与慢车行驶时间 之间的函数图象. 23. 实际情境:甲、乙两人从相距4千米的两地同时、同向出发,甲每小时走6千米,乙每小时走4千米,小狗随甲一起出发,每小时跑12千米,小狗遇到乙的时候它就往甲这边跑,遇到甲时又往乙这边跑,遇到乙的时候再往甲这边跑…就这样一直跑下去.
23. 实际情境:甲、乙两人从相距4千米的两地同时、同向出发,甲每小时走6千米,乙每小时走4千米,小狗随甲一起出发,每小时跑12千米,小狗遇到乙的时候它就往甲这边跑,遇到甲时又往乙这边跑,遇到乙的时候再往甲这边跑…就这样一直跑下去.数学研究:如图,折线、分别表示甲、小狗在行进过程中,离乙的路程y(km)与甲行进时间x(h)之间的部分函数图象.
 (1)、求线段AB对应的函数表达式;(2)、求点E的坐标;(3)、小狗从出发到它折返后第一次与甲相遇的过程中,直接写出x为何值时,它离乙的路程与它离甲的路程相等?24. 某工厂投资组建了日废水处理量为20吨的废水处理车间,已知该车间处理废水时每天需固定成本30元,并且每处理一吨废水还需费用8元.若该车间在无法完成当天工业废水的处理任务时,需将超出20吨的部分交给第三方企业处理。如图所示为该厂日废水处理总费用y(元)与该厂日产生的工业废水x(吨)之间的函数关系图象.
(1)、求线段AB对应的函数表达式;(2)、求点E的坐标;(3)、小狗从出发到它折返后第一次与甲相遇的过程中,直接写出x为何值时,它离乙的路程与它离甲的路程相等?24. 某工厂投资组建了日废水处理量为20吨的废水处理车间,已知该车间处理废水时每天需固定成本30元,并且每处理一吨废水还需费用8元.若该车间在无法完成当天工业废水的处理任务时,需将超出20吨的部分交给第三方企业处理。如图所示为该厂日废水处理总费用y(元)与该厂日产生的工业废水x(吨)之间的函数关系图象.
 (1)、求y关于x的函数关系式:(2)、设该厂日废水处理的平均费用为a元/吨,
(1)、求y关于x的函数关系式:(2)、设该厂日废水处理的平均费用为a元/吨,①当a=10时,在图1中画出直线y=ax的图象,结合图象判断直线y=ax与日废水处理总费用y的函数图象交点个数,求交点横坐标x的值并说明它的实际意义;
②当a=t时,参照上一小题的解法,求出该厂这日产生工业废水量x的值.