2022-2023初数北师大版八年级上册4.3一次函数的图象 同步练习
试卷更新日期:2022-07-24 类型:同步测试
一、单选题(每题3分,共30分)
-
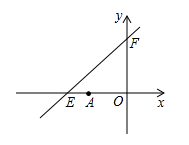
1. 如果正比例函数y=(a﹣1)x(a是常数)的图象在第一、三象限,那么a的取值范围是( )A、a>1 B、a<1 C、a<0 D、a>02. 对于函数 (k是常数, ),下列说法错误的是( )A、该函数是正比例函数 B、该函数图象过 C、该函数图象经过二、四象限 D、y随着x的增大而增大3. 对于函数y=-3x+1,下列结论正确的是( )A、它的图象必经过点(1,3) B、y的值随x值的增大而增大 C、当x>0时,y<0 D、它的图象与x轴的交点坐标为( , 0)4. 已知实数m<1,则一次函数y=(m﹣1)x+3﹣m图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、三、四 D、一、二、四5. 给出下列函数:①y=﹣3x+2;②y=;③y=2x2;④y=﹣5(x﹣1)2 , 上述函数中满足“当x>1时,函数值y随自变量x增大而增大”的是( )A、① B、② C、③ D、④6. 在平面直角坐标系中,若点(x1 , -1),(x2 , -2),(x3 , 1)都在直线y=-2x+b上,则x1 , x2 , x3的大小关系是( )A、x1>x2>x3 B、x3>x2>x1 C、x2>x1>x3 D、x2>x3>x17. 一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:
①对于函数y=ax+b来说,y随x的增大而减小;
②函数y=ax+d的图象不经过第一象限;
③不等式ax+b>cx+d的解集是x>3;
④d﹣b=3(a﹣c).其中正确的有( )
 A、①③ B、②③④ C、①②④ D、②③8. 若式子 有意义,则一次函数 的图象可能是( )A、
A、①③ B、②③④ C、①②④ D、②③8. 若式子 有意义,则一次函数 的图象可能是( )A、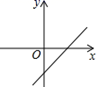 B、
B、 C、
C、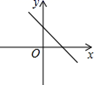 D、
D、 9. 把直线y=3x向下平移2个单位,得到的直线是( )A、y=3x﹣2 B、y=3(x﹣2) C、y=3x+2 D、y=3(x+2)10. 已知直线 交x轴于点 ,交 轴于点 ,直线 与直线 关于x轴对称,将直线 向下平移8个单位得到直线 ,则直线 与直线 的交点坐标为( )A、 B、 C、 D、
9. 把直线y=3x向下平移2个单位,得到的直线是( )A、y=3x﹣2 B、y=3(x﹣2) C、y=3x+2 D、y=3(x+2)10. 已知直线 交x轴于点 ,交 轴于点 ,直线 与直线 关于x轴对称,将直线 向下平移8个单位得到直线 ,则直线 与直线 的交点坐标为( )A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 已知正比例函数的图象上有两点、 , 若 , 则与的大小关系是.12. 已知 M(1, a )和 N(2, b )是一次函数 y=-x+1 图象上的两点,则 ab (填“>”、“<”或“=”).13. 一次函数 , 则函数在y轴上的截距为 .14. 请写出符合以下两个条件的一个函数解析式.①过点(-2,1),②在第二象限内,y随x增大而增大.15. 若y=(m-2)x|m-2|﹣5是关于x的一次函数,且y随x增大而减小,则常数m的值为.16. 在平面直角坐标系中,若将一次函数y=2x+m-1的图象向右平移3个单位后,得到一个正比例函数的图象,则m的值为 .
三、解答题(共8题,共52分)
-
17. 直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.

⑴写出A,B两点的坐标,并画出直线l的图象;
⑵将直线l向上平移4个单位得到l1 , l2交x轴于点C.作出l1的图象,并求l1的解析式.
18. 在平面直角坐标系中,判断A(1,3),B(-2,0),C(-4,-2)三点是否在同一直线上,并说明理由.19. 已知直线 与直线 的交点 的横坐标为3,与直线 的交点 的纵坐标为 ,求直线 的函数关系式.20. 已知y=y1+y2 , 其中y1与x﹣3成正比例,y2与x2+1成正比例,且当x=0时,y=﹣4,当x=﹣1时,y=﹣6.(1)、求y与x的函数关系式;(2)、判断点A(1,﹣4)是否在此函数图象上,并说明理由.21. 设函数y1=ax+b,y2=bx+a(a,b为常数,ab≠0且a≠b),函数y1和y2的图象的交点为点P.(1)、求点P的横坐标.(2)、已知点P在第一象限,函数y2的值随x的增大而增大.①当x=2时,y2﹣y1=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<
22. 已知一次函数的图象经过点 .(1)、求一次函数的表达式;(2)、若点 、 在一次函数的图象上, ,求a的取值范围;(3)、过原点O的直线恰好把 的面积分成相等的两部分,直接写出这条直线对应的函数表达式.