2022-2023初数北师大版八年级上册4.2一次函数与正比例函数同步练习

试卷更新日期：2022-07-24 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知函数y＝（m﹣2） $x^{m^{2} - 3}$ ＋1是一次函数，则m的值为（）

A、± $\sqrt{3}$ B、 $\sqrt{3}$ C、±2 D、﹣2

查看试题解析
2. 在①y＝－8x ， ②y＝ $- \frac{3}{x}$ ，③y＝x＋1，④y＝－5x²＋1，⑤y＝0.5x－3中，一次函数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列函数关系式： $① y = - 2 x$ ， $② y = - \frac{2}{x}$ ， $③ y = - 2 x^{2}$ ， $④ y = 2$ ， $⑤ y = 2 x - 1.$ 其中是一次函数的是（）

A、 $① ⑤$ B、 $① ④ ⑤$ C、 $② ⑤$ D、 $② ④ ⑤$

查看试题解析
4. 若 $y + 2$ 与 $x - 1$ 成正比例，则y是x的（）

A、一次函数 B、正比例函数 C、没有函数关系 D、以上答案都不正

查看试题解析
5. 下列函数：①y= $\frac{1}{2}$ x²-x；②y=-x+10；③y=2x；④y= $\frac{x}{2}$ -1．其中是一次函数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列函数中，是一次函数但不是正比例函数的是（）

A、y＝－ $\frac{x}{2}$ B、y＝－ $\frac{5}{x}$ C、y＝－ $\frac{x - 1}{2}$ D、y＝ $\frac{x^{2} - 1}{x}$

查看试题解析
7. 已知A，B两地相距3千米，小黄从A地到B地，平均速度为4千米/时，若用x表示行走的时间(小时)，y表示余下的路程(千米)，则y关于x的函数解析式是（）

A、y=4x(x≥0) B、y=4x-8(x≥ $\frac{3}{4}$ ) C、y=3-4x(x≥0) D、y=3-4z(0≤x≤ $\frac{3}{4}$ )

查看试题解析
8. 一辆汽车以每小时80km的速度从连云港开往相距300 km的南京，经过t h后距南京的路程为s km，则s与t的关系式为（）

A、s=80t B、s=300+ 80t C、s=300-80t D、s=80t-300

查看试题解析
9. 已知y是x-3的正比例函数，且当x=5时，y=6，则y和x的函数关系描述错误的是（）

A、y=3(x-3) ；是正比例函数关系 B、y=3x-9；是一次函数关系 C、y=3(x-3)；是一次函数关系 D、y=3x-9；是正比例函数关系

查看试题解析

10. 一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：

会员年卡类型	办卡费用/元	每次游泳收费/元
A类	50	25
B类	200	20
C类	400	15

例如，购买A类会员年卡，一年内游泳20次，消费50+25×20=550(元)，若一年内在该游泳馆游泳的次数介于45~55次之间，则最省钱的方式为（）

A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡

查看试题解析

二、填空题（每题3分，共18分）

11. 已知函数y＝（a+1）x+a²﹣1，当a时，它是一次函数；当a时，它是正比例函数．

查看试题解析
12. 已知 $y = (m + 2) x^{m^{2} - 3} + m + 1$ 是一次函数，则 $m =$ .

查看试题解析
13. 已知y与x-3成正比例，当x=4时，y=3，则y与x之间的函数表达式为。

查看试题解析
14. 已知 $y - 2$ 与 $x$ 成正比例，且当 $x = - 1$ 时， $y = 5,$ 则 $y$ 与 $x$ 的函数关系式为

查看试题解析
15. 定义[a，b]为一次函数y＝ax＋b(a≠0，a，b为实数)的“关联数”.若“关联数”[1，m－2]对应的一次函数是正比例函数，则关于x的方程 $\frac{1}{x - 1} + \frac{1}{m} = 1$ 的解为 .

查看试题解析
16. 下表中记录了一次试验中时间和温度的数据.

时间/分钟

0

5

10

15

20

25

温度/℃

10

25

40

55

70

85

若温度的变化是均匀的，则14分钟时的温度是℃.

查看试题解析

三、解答题（共8题，共52分）

17. 已知y-1与2x+3是正比例关系， y是关于x的一次函数吗?请说明理由.

查看试题解析
18. 已知函数 $y = (m - 2) x^{m^{2} - 3} + 4 + n$ .

(1)、当 $m, n$ 为何值时， $y$ 是 $x$ 的一次函数，并写出关系式；

(2)、当 $m, n$ 为何值时， $y$ 是 $x$ 的正比例函数，并写出关系式.

查看试题解析
19. 已知 $y + 3$ 与 $x$ 成正比例，且 $x = 2$ 时， $y = 1$ ．

(1)、求 $y$ 关于 $x$ 的函数表达式；

(2)、当 $x = - \frac{1}{2}$ 时，求 $y$ 的值．

查看试题解析

20. 某校计划从甲、乙两家体育用品店中选择一家购买一批乒乓球拍以丰富学生的校园生活．已知甲、乙两家体育用品店的每副乒乓球拍标价均为30元，现两家分别推出以下优惠方案：甲体育用品店：购买10副以上，从第11副开始按标价的七折出售；乙体育用品店：从第1副起就按标价的八五折出售．

设该校计划购买乒乓球拍的副数为x（x为正整数）

(1)、根据题意，填写下表：

购买副数	5	10	15	30	…
在甲体育用品店购买的费用（元）	150		405		…
在乙体育用品店购买的费用（元）	127.5		382.5		…

(2)、若该校计划用1581元购买乒乓球拍，则该校选择在哪一家体育用品店购买的兵乓球拍比较多？

(3)、当

x > 12

时，该校在哪家体育用品店购买更合算？并说明理由．

查看试题解析

21. 某家电商店计划购进并销售甲、乙两种品牌小家电，已知甲品牌家电每台进价为200元，售价为280元，乙品牌家电每台进价为400元，售价为500元，若该家电商店购进甲品牌家电x台，乙品牌家电y台，恰好花费20000元．

(1)、求y与x之间的函数关系式；

(2)、已知购买两种家电的总台数不超过60台，全部售完这些家电所获得的总利润为W元，求当 $x$ 为何值时，W最大，最大值是多少．

查看试题解析
22. 为了做好防疫工作，学校准备购进一批消毒液．已知A型消毒液7元/瓶，B型消毒液9元/瓶．学校准备购进这两种消毒液共90瓶．

(1)、写出购买所需总费用w元与A瓶个数x之间的函数表达式；

(2)、若B型消毒液的数量不少于A型消毒液数量的 $\frac{1}{3}$ ，请设计最省钱的购买方案，并求出最少费用．

查看试题解析
23. 如图，长方形ABCD中，BC=8，CD=5，点E为边AD上一动点，连接CE，随着点E的运动，四边形ABCE的面积也发生变化．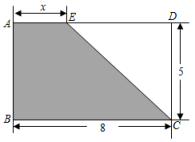

(1)、写出四边形ABCE的面积y与AE的长x（0＜x＜8）之间的关系式；

(2)、当x=3时，求y的值；

(3)、当四边形ABCE的面积为35时，求DE的长．

查看试题解析
24. 某剧院举行新年专场音乐会，成人票每张40元，学生票每张10元，剧院制定了两种优惠方案，且每个团体购票时只能选择其中一种优惠方案，方案1：购买一张成人票赠送一张学生票；方案2：按总价的90%付款．某校有4名老师与x（x≥4）名学生去观赏这次音乐会，设用方案1和方案2付款的总金额分别为y₁（元）和y₂（元）．

(1)、分别求出y₁、y₂与x之间的函数关系式；

(2)、当学生人数为20名时，请通过计算说明哪种方案更优惠；

(3)、请通过计算说明：当学生人数为多少时，选择两种方案一样优惠？

查看试题解析

时间/分钟	0	5	10	15	20	25
温度/℃	10	25	40	55	70	85

2022-2023初数北师大版八年级上册4.2一次函数与正比例函数 同步练习

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共52分）

2022-2023初数北师大版八年级上册4.2一次函数与正比例函数同步练习