2022-2023初数北师大版八年级上册4.1函数 同步练习
试卷更新日期:2022-07-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 函数y= 中,自变量x的取值范围是( )A、x≤5 B、x<5 C、x≥5 D、x>52. 当时,函数的值等于( )A、 B、 C、 D、3. 当时,函数的值是( )A、2 B、 C、 D、4. 下列各图中,不能表示y是x的函数的是( )A、
 B、
B、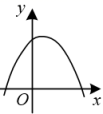 C、
C、 D、
D、 5. 下列各列表中,不能表示y是x的函数的是( )A、
5. 下列各列表中,不能表示y是x的函数的是( )A、
B、x 1 2 3 4 5 y 6 7 8 9 1
C、x 1 2 3 4 5 y 8 8 8 8 10
D、x 1 2 2 4 5 y 6 3 2 1 5 x 1 2 3 4 5 y 2 4 6 8 10 6. 某地海拔高度h与温度T的关系可用T=21-6h来表示(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为 ( )A、9 ℃ B、7 ℃ C、6 ℃ D、3 ℃7. 下列函数中,自变量的取值范围选取错误的是( )A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数 C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数8. 一次函数 的自变量的取值增加2,函数值就相应减少4,则k的值为( )A、2 B、-1 C、-2 D、49. 下面四个关系式:① ;② ;③ ;④ .其中 是 的函数的是( )A、①② B、②③ C、①②③ D、①③④10. 已知函数y= 当x=2时,函数值y为( )A、5 B、6 C、7 D、8二、填空题(每题3分,共18分)
-
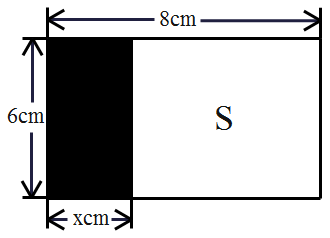
11. 若点A (5,m)是直线y= 2x 上一点,则m=.12. 如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为.
 13. 等腰三角形的顶角y与底角x之间是函数关系吗?(选是或不是)14. 已知函数y= , 当x=时,y= .15. 函数 ,则当函数自变量 时,y=16. 关于x,y的关系式:(1)y-x=0;(2)x=2y;(3)y2=2x;(4)y-x2=x,其中y是x的函数的是
13. 等腰三角形的顶角y与底角x之间是函数关系吗?(选是或不是)14. 已知函数y= , 当x=时,y= .15. 函数 ,则当函数自变量 时,y=16. 关于x,y的关系式:(1)y-x=0;(2)x=2y;(3)y2=2x;(4)y-x2=x,其中y是x的函数的是三、解答题(共8题,共52分)
-
17. 求下列函数中自变量的取值范围.(1)、(2)、(3)、(4)、(5)、18. 代数式2x+3中,当x取a﹣3时,问2x+3是不是a的函数?若不是,请说明理由;若是,也请说明理由,并请以a的取值为横坐标,对应的2x+3值为纵坐标,画出其图象.19. 求下列函数中自变量x的取值范围.y=+;20. 当x=2及x=﹣3时,分别求出下列函数的函数值:
(1)y=(x+1)(x﹣2);
(2)y= .
21. 等腰三角形的周长为80.(1)、写出底边长y与腰长x的函数表达式,并写出自变量的取值范围;(2)、当腰长为30时,底边长为多少?当底边长为8时,腰长为多少?22. 在国内投寄平信应付邮资如表:信件质量x(克)
0<x≤20
20<x≤40
40<x≤60
邮资y(元/封)
1.20
2.40
3.60
(1)、根据函数的定义,y是关于x的函数吗?(2)、结合表格解答:①求出当x=48时的函数值,并说明实际意义.
②当寄一封信件的邮资是2.40元时,信件的质量大约是多少克?
23. 周末了,小红带弟弟一起荡秋千,秋千离地面的高度 与摆动时间 之间的关系如图所示.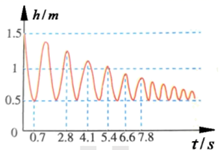 (1)、根据函数的定义,请判断变量h是否为t的函数?(2)、当 时,h的值是多少?并说明它的实际意义;(3)、秋千摆动第二个来回需要多少时间?24. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
(1)、根据函数的定义,请判断变量h是否为t的函数?(2)、当 时,h的值是多少?并说明它的实际意义;(3)、秋千摆动第二个来回需要多少时间?24. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.x
…
1
2
4
5
6
8
9
…
y
…
3.92
1.95
0.98
0.78
2.44
2.44
0.78
…
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
 (1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=7对应的函数值y约为 .
②该函数的一条性质: .