2022-2023学年浙教版数学九年级上册4.5 相似三角形的性质及应用 同步练习
试卷更新日期:2022-07-24 类型:同步测试
一、单选题
-
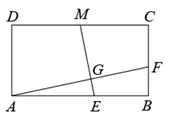
1. 如图,在矩形ABCD中,AB=2BC,点M是CD边的中点,点E,F分别是边AB,BC上的点,且AF⊥ME,G为垂足.若EB=2,BF=1,则四边形BFGE的面积为( )
 A、 B、 C、 D、2. 如图, 在圆形方格网横线上, 点 是直径 与网格横线的交点, 则 为( )
A、 B、 C、 D、2. 如图, 在圆形方格网横线上, 点 是直径 与网格横线的交点, 则 为( ) A、 B、 C、 D、3. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )
A、 B、 C、 D、3. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )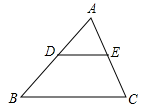 A、8 B、12 C、14 D、164.
A、8 B、12 C、14 D、164.
如图,平行四边形OABC的顶点O(0,0),A(1,2),点C在x轴的正半轴上,延长BA交y轴于点D.将△ODA绕点O顺时针旋转得到△OD'A',当点D的对应点D'落在OA上时,D'A'的延长线恰好经过点C,则点B的坐标为( ) A、(2 , 2) B、(2 , 2) C、(2 1,2) D、(2 1,2)5. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )
A、(2 , 2) B、(2 , 2) C、(2 1,2) D、(2 1,2)5. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )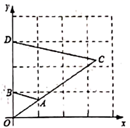 A、 B、 C、 D、6. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边 cm, cm,测得边DF离地面的高度 m, m,则树高AB为( )
A、 B、 C、 D、6. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边 cm, cm,测得边DF离地面的高度 m, m,则树高AB为( )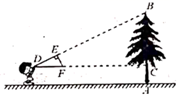 A、4m B、5m C、5.5m D、6.5m7. 如图, 中, 是 的中位线,连接 , 相交于点 ,若 ,则 为( )
A、4m B、5m C、5.5m D、6.5m7. 如图, 中, 是 的中位线,连接 , 相交于点 ,若 ,则 为( )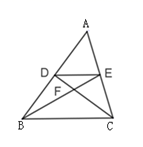 A、3 B、4 C、9 D、128. 如图, ABC与 DEF位似,点O是位似中心,若OE=3OB, =4,则 =( )
A、3 B、4 C、9 D、128. 如图, ABC与 DEF位似,点O是位似中心,若OE=3OB, =4,则 =( ) A、9 B、12 C、16 D、369. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )
A、9 B、12 C、16 D、369. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )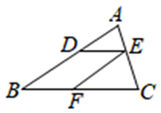 A、 B、 C、 D、10. 如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )
A、 B、 C、 D、10. 如图,在△ABC中,DE∥BC, = ,则下列结论中正确的是( )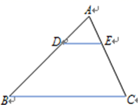 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
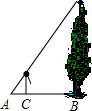
11. 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为米.
 12. 如图,双曲线 经过Rt 斜边上的中点A,与BC交于点D, ,则 .
12. 如图,双曲线 经过Rt 斜边上的中点A,与BC交于点D, ,则 .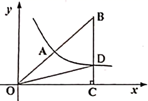 13. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE:AD =2:3,CD=2,则AF的长为.
13. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE:AD =2:3,CD=2,则AF的长为.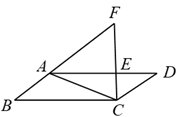 14. 如图,l1∥l2∥l3 , 若AB=2,BC=3,AD=1,CF=4,则BE的长为.
14. 如图,l1∥l2∥l3 , 若AB=2,BC=3,AD=1,CF=4,则BE的长为. 15. 如图,在⊙O中, = ,AB=10,BC=12,D是 上一点,CD=5,则AD的长为.
15. 如图,在⊙O中, = ,AB=10,BC=12,D是 上一点,CD=5,则AD的长为. 16. 如图,在直角∆ABC中,∠C=90°,AC=8,BC=6,点M从点C出发沿线段CA向点A移动,连接BM,MN⟂BM交边AB于点N.若CM=2,那么线段AN=;当点M从点C移动到AC的中点时,则点N的运动过程中路径长为。
16. 如图,在直角∆ABC中,∠C=90°,AC=8,BC=6,点M从点C出发沿线段CA向点A移动,连接BM,MN⟂BM交边AB于点N.若CM=2,那么线段AN=;当点M从点C移动到AC的中点时,则点N的运动过程中路径长为。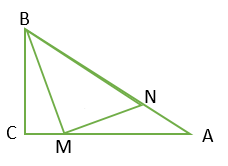
三、解答题
-
17. 某校初三年级在一次研学活动中,数学研学小组为了估计澧水河某段水域的宽度,在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C ,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE BC.经测量BC=25米,BD=12米,DE=35米,求河的宽度AB为多少米?
 18. 如图, , 、相交于点O,若 , , . 求的长度.
18. 如图, , 、相交于点O,若 , , . 求的长度.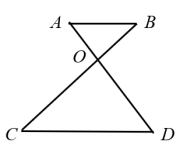 19. 已知:如图,、分别是的边、上的点, , , , . 求的长度.
19. 已知:如图,、分别是的边、上的点, , , , . 求的长度. 20. 如图,在△ABC中,AD平分∠BAC交BC于点D,DE∥AC交AB于点E,求证: .
20. 如图,在△ABC中,AD平分∠BAC交BC于点D,DE∥AC交AB于点E,求证: . 21. 如图,在正方形ABCD中,M为BC上一点, ,ME交CD于F,交AD的延长线于点E.
21. 如图,在正方形ABCD中,M为BC上一点, ,ME交CD于F,交AD的延长线于点E.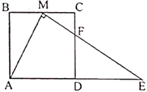 (1)、求证: ;(2)、若 , ,求 的面积.22. 在 中, , 垂直平分 ,分别交 于点 .
(1)、求证: ;(2)、若 , ,求 的面积.22. 在 中, , 垂直平分 ,分别交 于点 . (1)、求证: ;(2)、求证: .23. 如图,在 中, , cm, cm,点P由点B出发沿BA的方向向点A匀速运动,速度为1cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ.设运动的时间为t(s),其中 .解答下列问题:
(1)、求证: ;(2)、求证: .23. 如图,在 中, , cm, cm,点P由点B出发沿BA的方向向点A匀速运动,速度为1cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ.设运动的时间为t(s),其中 .解答下列问题: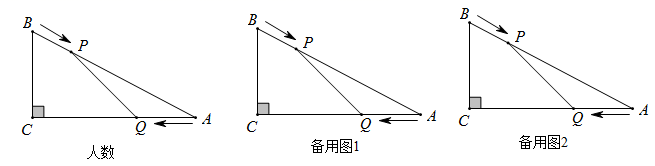 (1)、AP= , AQ=;(用含t的代数式表示)(2)、当t为何值时, ∽ ;(3)、当P、Q在运动过程中, 能否成为等腰三角形?若能,求出此时t的值;若不能,请说明理由.24. 如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.
(1)、AP= , AQ=;(用含t的代数式表示)(2)、当t为何值时, ∽ ;(3)、当P、Q在运动过程中, 能否成为等腰三角形?若能,求出此时t的值;若不能,请说明理由.24. 如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE. (1)、探索发现:
(1)、探索发现:图1中,的值为 , 的值为.
(2)、拓展探究若将△CDE绕点C旋转,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.
(3)、问题解决当△CDE旋转至A,D,C三点共线时,直接写出线段BE的长.