2022-2023学年浙教版数学九年级上册4.3 相似三角形 同步练习
试卷更新日期：2022-07-24 类型：同步测试
一、单选题
-
1. 如图，已知△ABC∽△ACP，∠A＝70°，∠APC＝65°，则∠B的度数为（ ）
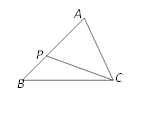A、45° B、50° C、55° D、60°2. 如图，已知△ABC∽△DEF，若∠A＝35°，∠B＝65°，则∠F的度数是（ ）
A、30° B、35° C、80° D、100°3. 如图，△ABO∽△CDO，若BO＝8，DO＝4，CD＝3，则AB的长是（ ）
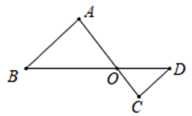A、2 B、3 C、4 D、64. 如图，已知 ， 若 ， ， ， 则AC的长是（ ）
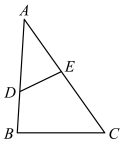A、12 B、13 C、14 D、155. 已知 ， ， 则=（ ）A、2 B、 C、3 D、6. 已知的三边长是 ， ， 2，则与相似的三角形的三边长可能是（ ）A、1， ， B、1， ， C、1， ， D、1， ，7. △ABC中，AB=6，BC=10，CA=12，另一个和它相似的三角形最长的一边是36，则最短的一边是（ ）A、12 B、18 C、20 D、278. 要制作两个形状相同的三角形框架，其中一个三角形的边长分别为8cm，10cm和12cm，另一个三角形的最短边长为2cm，则它的最长边为（ ）A、3cm B、4cm C、4.5cm D、5cm9. 已知△ABC如图，则下列4个三角形中，与△ABC相似的是（ ）
A、
B、
C、
D、
10. 如图所示， ，则 的度数为（ ）
A、 B、 C、 D、11. 如图，在正方形网格中：△ABC、△EDF的顶点都在正方形网格的格点上，△ABC∽△EDF ， 则∠ABC＋∠ACB的度数为（ ）
A、75° B、60° C、55° D、45°12. 如图，已知△ABC和△A′B′C′相似，则图中角度 和边长x分别为（ ）
A、30°，9 B、30°，6 C、40°，9 D、40°，6二、填空题
-
13. 如图，在中， ， ， D是的中点，过D点的直线交于点Q，若使与相似，则的长度为 ．
14. 如图所示，已知AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC相似，则AP= ．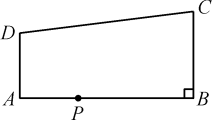
15. 如图，矩形ABCD中，AD＝4，AB＝10，P为CD边上的动点，当DP＝时，△ADP与△BCP相似．
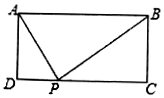16. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面 .
17. 如图，点C、D在线段AB上，△PCD是等边三角形．当△ACP∽△PDB时，∠APB＝°．
18. 如图，△ABC∽△DAC，∠B＝28°，∠D＝140°，则∠BAD的度数为.
三、解答题
-
19. 如图，在△ABC中，AB＝10cm，BC＝20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果点P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．
20. 如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB＝6，AE＝9，DE＝2，求EF的长.
21.(1)、已知 ，求一次函数 所经过的象限；(2)、已知 与 相似，且 的三边长分别为6、8、4， 其中一边长为2，试求 的另外两边长．22. 如果三角形的两个内角 与 满足 =90°，那么我们称这样的三角形为“准互余三角形”．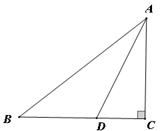
(1)、若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，求∠B的度数；(2)、如图①，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝5，若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．23. 如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t >0）秒．
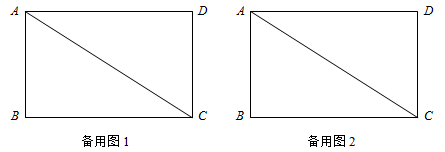(1)、当点Q从B点向A点运动时（未到达A点），若△APQ ∽△ABC，求t的值；(2)、伴随着P，Q两点的运动，线段PQ的垂直平分线为直线l．①当直线l经过点A时，射线QP交AD边于点E，求AE的长；
②是否存在t的值，使得直线l经过点B？若存在，请求出所有t的值；若不存在，请说明理由．