2022-2023学年浙教版数学九年级上册4.2 由平行线截得的比例线段 同步练习
试卷更新日期:2022-07-24 类型:同步测试
一、单选题
-
1. 如图, ,直线a,b与 分别交于点A、B、C和点D、E、F,若AB∶BC=2∶3,EF=6,则DE的长是( )
 A、8 B、9 C、4 D、102. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=4,BC=6,EF=9,则DE的长为( )
A、8 B、9 C、4 D、102. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=4,BC=6,EF=9,则DE的长为( ) A、3 B、4 C、5 D、63. 如图, , BC=2, , 则AB的长为( )
A、3 B、4 C、5 D、63. 如图, , BC=2, , 则AB的长为( ) A、6 B、5 C、4 D、34. 如图 中, 分别在边 上, , 则 ( )
A、6 B、5 C、4 D、34. 如图 中, 分别在边 上, , 则 ( ) A、6 B、12 C、18 D、245. 如图, , 直线与这三条平行线分别交于点A、B、C和点D、E、F,若 , 则DE的长度是( )
A、6 B、12 C、18 D、245. 如图, , 直线与这三条平行线分别交于点A、B、C和点D、E、F,若 , 则DE的长度是( ) A、 B、 C、6 D、106. 如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( )
A、 B、 C、6 D、106. 如图,在△ABC中,DE∥BC,AD=4,DB=2,AE=3,则EC的长为( ) A、 B、1 C、2 D、7. 如图,在中,点 , , 分别在边 , , 上,且 , , 若 , 则的值为( )
A、 B、1 C、2 D、7. 如图,在中,点 , , 分别在边 , , 上,且 , , 若 , 则的值为( )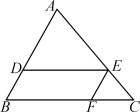 A、 B、 C、 D、8. 如图, , 若 , 则的值是( )
A、 B、 C、 D、8. 如图, , 若 , 则的值是( )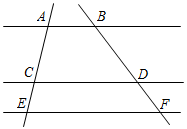 A、2 B、 C、 D、39. 在中,点E、D、F分别在边AB、BC、AC上,联结DE、DF,如果 , , , 那么的值是( )A、 B、 C、 D、10. 如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( )
A、2 B、 C、 D、39. 在中,点E、D、F分别在边AB、BC、AC上,联结DE、DF,如果 , , , 那么的值是( )A、 B、 C、 D、10. 如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,已知△ABC中,点D在AB上,点E在AC上,DE∥BC.AD=2,DB=3,AE=4,则EC=;
 12. 如图,在ΔABC中,BC=20,点B1 , B2 , B3 , B4和点C1 , C2 , C3 , C4分别是AB,AC的5等分点,则B1C1+B2C2+B3C3+B4C4的值为。
12. 如图,在ΔABC中,BC=20,点B1 , B2 , B3 , B4和点C1 , C2 , C3 , C4分别是AB,AC的5等分点,则B1C1+B2C2+B3C3+B4C4的值为。 13. 如图,已知▱ABCD的对角线AC、BD交于点O,DE平分∠ADC交BC于点E,交AC于点F,且∠BCD=60°,BC=2CD,连结OE.下列结论,①OE//CD;②OE=CD;③S▱ABCD=BD·CD;④AO=2BO,⑤S△DOF=2S△EOF.其中正确结论的序号是;
13. 如图,已知▱ABCD的对角线AC、BD交于点O,DE平分∠ADC交BC于点E,交AC于点F,且∠BCD=60°,BC=2CD,连结OE.下列结论,①OE//CD;②OE=CD;③S▱ABCD=BD·CD;④AO=2BO,⑤S△DOF=2S△EOF.其中正确结论的序号是; 14. 如图,已知l1∥l2∥l3 , 直线AB分别交l1、l2、l3于A、M、B,直线CD分别交l1、l2、l3于C、N、D,AM=4,MB=6,CD=9,那么ND= .
14. 如图,已知l1∥l2∥l3 , 直线AB分别交l1、l2、l3于A、M、B,直线CD分别交l1、l2、l3于C、N、D,AM=4,MB=6,CD=9,那么ND= . 15. 我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形ABCD中,ADBC,AD=1,BC=2,E、F分别是边AB、CD上的点,且EFBC,如果四边AEFD与四边形EBCF相似,那么的值是 .
15. 我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形ABCD中,ADBC,AD=1,BC=2,E、F分别是边AB、CD上的点,且EFBC,如果四边AEFD与四边形EBCF相似,那么的值是 .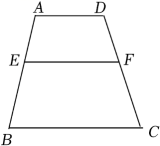 16. 如图,A,B两点在x轴上,点P为反比例函数图象上一点,连接 , , , 且与反比例函数的图象交于点N,若 , , 的面积为2,则k的值为 .
16. 如图,A,B两点在x轴上,点P为反比例函数图象上一点,连接 , , , 且与反比例函数的图象交于点N,若 , , 的面积为2,则k的值为 .
三、解答题
-
17. 如图,在中,点D为边上一点,连接 , 点H为中点,延长交边于点E,求证: .
 18. 如图,在△ABC中,EF∥CD ,DE∥BC .求证:AF:FD=AD:DB .
18. 如图,在△ABC中,EF∥CD ,DE∥BC .求证:AF:FD=AD:DB .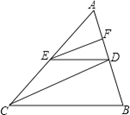 19. 在四边形ABCD中, , , , , 的平分线分别交AD、AC于点E、F,求 的值.
19. 在四边形ABCD中, , , , , 的平分线分别交AD、AC于点E、F,求 的值. 20. 如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
20. 如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?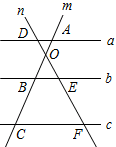 21. 如图,在△ABC中,EFCD,DEBC.
21. 如图,在△ABC中,EFCD,DEBC. (1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.22. 如图,已知在平面直角坐标系xOy中,抛物线y=(x﹣2)2的顶点为C,与y轴正半轴交于点B,一次函数y=kx+4(k≠0)图象与抛物线交于点A、点B,与x轴负半轴交于点D,若AB=3BD.
(1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.22. 如图,已知在平面直角坐标系xOy中,抛物线y=(x﹣2)2的顶点为C,与y轴正半轴交于点B,一次函数y=kx+4(k≠0)图象与抛物线交于点A、点B,与x轴负半轴交于点D,若AB=3BD.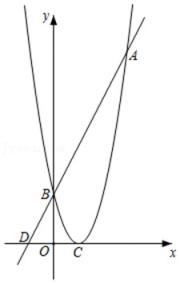 (1)、求点A的坐标;(2)、联结AC、BC,求△ABC的面积;(3)、如果将此抛物线沿y轴正方向平移,平移后的图象与一次函数y=kx+4(k≠0)图象交于点P,与y轴相交于点Q,当PQ∥x轴时,试问该抛物线平移了几个单位长度?
(1)、求点A的坐标;(2)、联结AC、BC,求△ABC的面积;(3)、如果将此抛物线沿y轴正方向平移,平移后的图象与一次函数y=kx+4(k≠0)图象交于点P,与y轴相交于点Q,当PQ∥x轴时,试问该抛物线平移了几个单位长度?

