2022-2023学年浙教版数学九年级上册3.7 正多边形 同步练习
试卷更新日期：2022-07-23 类型：同步测试
一、单选题
-
1. 如图四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转72°后，能与原图形完全重合的是（ ）A、
B、
C、
D、
2. ⊙O半径为4，以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形，则所得三角形的面积是（ ）A、2 B、 C、2 D、23. 如图，是正方形的外接圆，若的半径为4，则正方形的边长为（ ）
A、4 B、8 C、 D、4. 如图，正六边形内接于圆O，半径为4，则这个正六边形的边心距为（ ）
A、2 B、 C、 D、5. 圆内接正方形的面积为a，则圆的面积为（ ）A、 B、2πa C、 D、πa26. 若正六边形的周长为24，则它的外接圆的半径为（ ）A、4 B、4 C、2 D、27. 阅读图中的材料，解答下面的问题：已知⊙O是一个正十二边形的外接圆，该正十二边形的半径为2，如果用它的面积来近似估计⊙O的面积，则⊙O的面积大约是（ ）
A、12 B、12.4 C、12.56 D、8. 如图，正五边形ABCDE内接于⊙O，连接AC，则∠BAC的度数是（ ）
A、45° B、38° C、36° D、30°9. 如图，正方形ABCD内接于⊙O，点P在 上，则∠BPC的度数为（ ）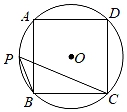
A、30° B、45° C、60° D、90°10. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（ ）．A、 B、 C、 D、二、填空题
-
11. 如图，在⊙O中，AB是⊙O的内接正六边形的一边，BC是⊙O的内接正十边形的一边，则∠ABC＝°.
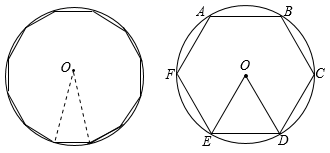
12. 如图，在圆内接正六边形ABCDEF中，半径OA=4，则这个正六边形的边长为 ．
13. 一个圆内接正多边形的一条边所对的圆心角是60°，则该正多边形边数是.14. 斛是中国古代的一种量器.据《汉书 .律历志》记载：“斛底，方而圜（huán）其外，旁有庣（tiāo）焉”．意思是说：“斛的底面为：正方形外接一个圆，此圆外是一个同心圆” . 如图所示，问题：现有一斛，其底面的外圆直径为两尺五寸（即2.5尺），“庣旁”为两寸五分（即两同心圆的外圆与内圆的半径之差为0.25尺），则此斛底面的正方形的边长为尺．
15. 是的内接正六边形一边，点P是优弧上的一点（点P不与点A，B重合）且 ， 与交于点C，则的度数为 ．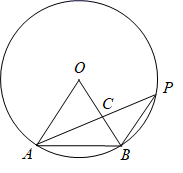
16. 如图，已知正方形ABCD和正△EGF都内接于⊙O，当EF∥BC时，的度数为 .
三、解答题
-
17. 已知圆内接正十二边形的面积为S，求同圆的内接正六边形的面积．
18. 如图，正五边形 内接于 ， 为 上的一点（点 不与点 重合），求 的余角的度数．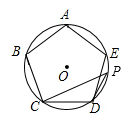
19. 如图，已知圆O内接正六边形 的边长为 ，求这个正六边形的边心距n ， 面积S ．
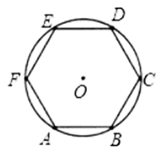20. 如图， 是 的内接正五边形．求证： .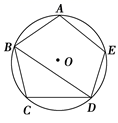
四、综合题
-
21. 如图，六边形ABCDEF是的内接正六边形.
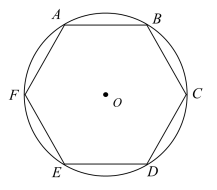(1)、求证：在六边形ABCDEF中，过顶点A的三条对角线四等分.(2)、设的面积为 ， 六边形ABCDEF的面积为 ， 求的值.22. 圆周率 的故事我国古代数学家刘徽通过“割圆术”来估计圆周率 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 的值.
(1)、对于边长为a的正方形，其外接圆半径为 ， 根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 ，可以估算 .(2)、类比（1），当正多边形为正六边形时，估计 的值.
