2022-2023学年浙教版数学九年级上册3.5 圆周角 同步练习
试卷更新日期:2022-07-23 类型:同步测试
一、单选题
-
1. 如图,⊙O是△ABC的外接圆,∠BOC=110°,则∠A的度数为( )
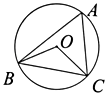 A、65° B、55° C、70° D、30°2. 如图,点A、B、C在⊙O上,∠CAB=70°,则∠BOC等于( )
A、65° B、55° C、70° D、30°2. 如图,点A、B、C在⊙O上,∠CAB=70°,则∠BOC等于( ) A、100° B、110° C、130° D、140°3. 以为中心点的量角器与直角三角板按如图方式摆放,量角器的0刻度线与斜边重合.点为斜边上一点,作射线交弧于点 , 如果点所对应的读数为 , 那么的大小为( )
A、100° B、110° C、130° D、140°3. 以为中心点的量角器与直角三角板按如图方式摆放,量角器的0刻度线与斜边重合.点为斜边上一点,作射线交弧于点 , 如果点所对应的读数为 , 那么的大小为( ) A、 B、 C、 D、4. 如图, 是 的直径, 是弦, , 则 的度数是( )
A、 B、 C、 D、4. 如图, 是 的直径, 是弦, , 则 的度数是( )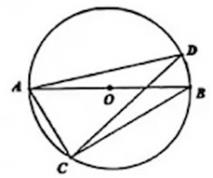 A、 B、 C、 D、5. 如图, 中的半径为1, 内接于 .若 , ,则 的长是( )
A、 B、 C、 D、5. 如图, 中的半径为1, 内接于 .若 , ,则 的长是( ) A、 B、 C、 D、6. 如图,AB,CD是⊙O的弦,且 ,若 ,则 的度数为( )
A、 B、 C、 D、6. 如图,AB,CD是⊙O的弦,且 ,若 ,则 的度数为( )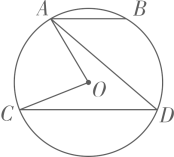 A、30° B、40° C、45° D、60°7. 如图,△ABC的外接圆半径为8,∠ACB=60°,则AB的长为( )
A、30° B、40° C、45° D、60°7. 如图,△ABC的外接圆半径为8,∠ACB=60°,则AB的长为( )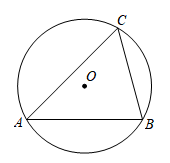 A、8 B、4 C、6 D、48. 如图,内接于 , 是的直径, , 则的度数是( )
A、8 B、4 C、6 D、48. 如图,内接于 , 是的直径, , 则的度数是( )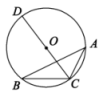 A、36° B、34° C、56° D、78°9. 如图,是⊙O的弦,且 , 点是弧中点,点是优弧上的一点, , 则圆心到弦的距离等于( )
A、36° B、34° C、56° D、78°9. 如图,是⊙O的弦,且 , 点是弧中点,点是优弧上的一点, , 则圆心到弦的距离等于( ) A、 B、 C、 D、10. 如图,AD为的直径, , , 则AC的长度为( )
A、 B、 C、 D、10. 如图,AD为的直径, , , 则AC的长度为( ) A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
11. 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC,若弦BC的长度为 ,则∠BAC=度.
 12. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,OH=1,则⊙O的半径是.
12. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,OH=1,则⊙O的半径是. 13. 如图,CD是⊙O的直径,AB是弦,CD⊥AB于点E,若OA=5,AB=8,则AD的长为 .
13. 如图,CD是⊙O的直径,AB是弦,CD⊥AB于点E,若OA=5,AB=8,则AD的长为 . 14. 如图,AB是的直径, , BC交于点D,AC交于点E, , 则°.
14. 如图,AB是的直径, , BC交于点D,AC交于点E, , 则°. 15. 如图,AB是半圆的直径,C、D是半圆上的两点,∠CAB=24°,则∠ADC的度数为 .
15. 如图,AB是半圆的直径,C、D是半圆上的两点,∠CAB=24°,则∠ADC的度数为 . 16. 如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是
16. 如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是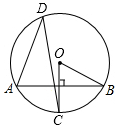
三、解答题
-
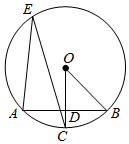
17. 如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB的长.
 18. 如图,是的外接圆⊙O的直径,若∠ACB=50°,求∠BAD的度数.
18. 如图,是的外接圆⊙O的直径,若∠ACB=50°,求∠BAD的度数. 19. 如图,是上的四个点,.判断的形状,并证明你的结论.
19. 如图,是上的四个点,.判断的形状,并证明你的结论. 20. 如图,在△ABC中,AC=BC,以AB为直径的⊙O分别交AC,BC于点E,F.
20. 如图,在△ABC中,AC=BC,以AB为直径的⊙O分别交AC,BC于点E,F.求证: .

四、综合题
-
21. 如图1, ABC中,AC=BC=4,∠ACB=90°,过点C任作一条直线CD,将线段BC沿直线CD翻折得线段CE,直线AE交直线CD于点F.直线BE交直线CD于G点.
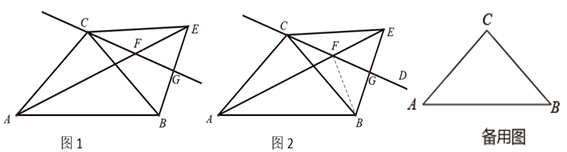 (1)、小智同学通过思考推得当点E在AB上方时,∠AEB的角度是不变的,请按小智的思路帮助小智完成以下推理过程:
(1)、小智同学通过思考推得当点E在AB上方时,∠AEB的角度是不变的,请按小智的思路帮助小智完成以下推理过程:∵AC=BC=EC,
∴A、B、E三点在以C为圆心以AC为半径的圆上,
∴∠AEB= ∠ACB,(填写数量关系)
∴∠AEB= °.
(2)、如图2,连接BF,求证A、B、F、C四点共圆;(3)、线段AE最大值为 , 若取BC的中点M,则线段MF的最小值为 .22. 如图,中, , 按要求完成下列问题: (1)、作出的外接圆;(要求用尺规作图,保留作图痕迹,不要求写出作法);(2)、在(1)的条件下,若CD平分 , CD交于点D,连接AD,BD.求证: .23. 如图,O为半圆的圆心,C、D为半圆上的两点,连接CD、BD、AD,.连接AC并延长,与BD的延长线相交于点E.
(1)、作出的外接圆;(要求用尺规作图,保留作图痕迹,不要求写出作法);(2)、在(1)的条件下,若CD平分 , CD交于点D,连接AD,BD.求证: .23. 如图,O为半圆的圆心,C、D为半圆上的两点,连接CD、BD、AD,.连接AC并延长,与BD的延长线相交于点E. (1)、求证:;(2)、若 , 半径 , 求BD的长.24. 在一次数学探究活动中,王老师设计了一份活动单:已知线段 , 使用作图工具作 , 尝试操作后思考:这样的点A唯一吗?点A的位置有什么特征?你有什么感悟?
(1)、求证:;(2)、若 , 半径 , 求BD的长.24. 在一次数学探究活动中,王老师设计了一份活动单:已知线段 , 使用作图工具作 , 尝试操作后思考:这样的点A唯一吗?点A的位置有什么特征?你有什么感悟?“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
 (1)、小华同学提出了下列问题,请你帮助解决.
(1)、小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为;
② 面积的最大值为;
(2)、经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形外部,我们记为 , 请你利用图1证明 .(3)、请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , , 点P在直线CD的左侧,且 , 则线段PB长的最小值为.