2022-2023初数北师大版八年级上册第二章实数 章末检测
试卷更新日期:2022-07-23 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 在数字 , π,0,2.121121112…(相邻两个2之间1的个数逐次多1)中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个2. (﹣3) 2的平方根是( )A、3 B、﹣3 C、 D、±33. 下列说法正确的是( ).A、4是 的算术平方根 B、0的算术平方根是0 C、-2是 算术平方根 D、-4的算术平方根是-24. 下列运算中正确的是( )A、 B、 C、 D、5. 估计 的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间6. 利用如图所示的计算器进行计算,按键操作错误的是( )
 A、计算 的值,按键顺序为
A、计算 的值,按键顺序为 B、计算 的值,按键顺序为
B、计算 的值,按键顺序为  C、计算 的值,按键顺序为
C、计算 的值,按键顺序为  D、计算器显示结果为 时,若按
D、计算器显示结果为 时,若按  键,则结果切换为小数格式0.333 333 333
7. 若将三个数- , , 表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
键,则结果切换为小数格式0.333 333 333
7. 若将三个数- , , 表示在数轴上,其中能被如图所示的墨迹覆盖的数是( ) A、- B、 C、 D、无法确定8. 在式子 中,二次根式有( )A、2个 B、3个 C、4个 D、5个9. 下列计算正确的是( )A、(+2)2=7 B、3﹣=3 C、=25 D、=510. 如图.从一个大正方形中裁去面积为8m2和18cm2的两个小正方形,则留下的阴影部分的面积为( )
A、- B、 C、 D、无法确定8. 在式子 中,二次根式有( )A、2个 B、3个 C、4个 D、5个9. 下列计算正确的是( )A、(+2)2=7 B、3﹣=3 C、=25 D、=510. 如图.从一个大正方形中裁去面积为8m2和18cm2的两个小正方形,则留下的阴影部分的面积为( )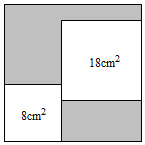 A、 cm2 B、 cm2 C、 cm2 D、 cm2
A、 cm2 B、 cm2 C、 cm2 D、 cm2二、解答题(共8题,共66分)
-
11. 用计算器计算下列各式的值(精确到0.001):(1)、;(2)、;(3)、;(4)、.12. 把下列各数填入相应的集合内:
,4, , , ,0.15,-7.5,- ,0,2.3.
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
13. 在下面数轴上作出﹣ 对应的点,尺规作图,保留必要的作图痕迹. 14. 计算:(1)、 ;(2)、 .15.(1)、已知:2a+1的算术平方根是3,3a﹣b﹣1的立方根是2,求 的值.(2)、已知a是 的整数部分,b是它的小数部分,求a2+(b+3)2的值.16. 材料1:因为无理数是无限不循环小数,所以无理数的小数部分我们不可能全部写出来.比如:π, 等,而常用的“…”或者“≈”的表示方法都不够百分百准确.
14. 计算:(1)、 ;(2)、 .15.(1)、已知:2a+1的算术平方根是3,3a﹣b﹣1的立方根是2,求 的值.(2)、已知a是 的整数部分,b是它的小数部分,求a2+(b+3)2的值.16. 材料1:因为无理数是无限不循环小数,所以无理数的小数部分我们不可能全部写出来.比如:π, 等,而常用的“…”或者“≈”的表示方法都不够百分百准确.材料2:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5−2得来的.
材料3:任何一个无理数,都夹在两个相邻的整数之间,如 ,是因为 .
根据上述材料,回答下列问题:
(1)、 的整数部分是 , 小数部分是.(2)、 也是夹在相邻两个整数之间的,可以表示为 ,求 的值.(3)、已知 ,其中x是整数,且0<y<1,求x+4y的倒数.17. 阅读下面的文字,解答问题.现规定:分别用和表示实数x的整数部分和小数部分,如实数3.14的整数部分是 , 小数部分是;实数的整数部分是 , 小数部分是无限不循环小数,无法写完整,但是把它的整数部分减去,就等于它的小数部分,即就是的小数部分,所以 .
(1)、 , ; , .(2)、如果 , , 求的立方根.18. 小石根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小石的探究过程,请补充完整:
(1)、具体运算,发现规律.特例1: ,
特例2: ,
特例3: ,
特例4: ,
特例5:(填写运算结果).
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为: .
(3)、证明你的猜想.(4)、应用运算规律.①化简:;
②若(a,b均为正整数),则的值为 .
三、填空题(共6题,共26分)