2022-2023学年浙教版数学九年级上册3.3 垂径定理 同步练习
试卷更新日期:2022-07-23 类型:同步测试
一、单选题
-
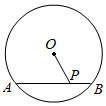
1. 如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
 A、3.1 B、4.2 C、5.3 D、6.42. 如图,AB是的弦,OC⊥AB于点C,连结OB,P是半径OB上任意一点,连结AP,若OB=5,OC=3,则AP的长不可能是( ).
A、3.1 B、4.2 C、5.3 D、6.42. 如图,AB是的弦,OC⊥AB于点C,连结OB,P是半径OB上任意一点,连结AP,若OB=5,OC=3,则AP的长不可能是( ). A、6 B、7 C、8 D、93. 如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( )
A、6 B、7 C、8 D、93. 如图,在⊙O中,半径OC⊥AB于点D.已知OC=5,OD=4,则弦AB的长为( ) A、3 B、4 C、5 D、64. 如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( )
A、3 B、4 C、5 D、64. 如图,在⊙O中,CD是⊙O的直径,AB⊥CD于点E,若AB=8,CE=2,则⊙O的半径为( ) A、 B、 C、3 D、55. 如图,在⊙O中,OC⊥AB,若∠BOC=40°,则∠OAB等于( )
A、 B、 C、3 D、55. 如图,在⊙O中,OC⊥AB,若∠BOC=40°,则∠OAB等于( ) A、40° B、50° C、80° D、120°6. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A、40° B、50° C、80° D、120°6. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )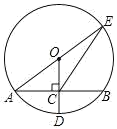 A、2 B、8 C、2 D、27. 在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm
A、2 B、8 C、2 D、27. 在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm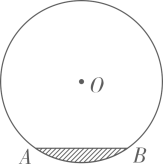 A、1 B、3 C、3或4 D、1或78. 往直径为78cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 , 则水的最大深度为( )
A、1 B、3 C、3或4 D、1或78. 往直径为78cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 , 则水的最大深度为( ) A、36 cm B、27 cm C、24 cm D、15 cm9. 半径等于4的圆中,垂直平分半径的弦长为( )A、 B、 C、 D、10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( )
A、36 cm B、27 cm C、24 cm D、15 cm9. 半径等于4的圆中,垂直平分半径的弦长为( )A、 B、 C、 D、10. 如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AD,若AB=10,CD=8,则AD的长为( ) A、8 B、2 C、3 D、4
A、8 B、2 C、3 D、4二、填空题
-
11. 如图,舞台地面上有一段以点O为圆心的 , 某同学要站在的中点C的位置上.于是他想:只要从点O出发,沿着与弦垂直的方向走到上,就能找到的中点C,老师肯定了他的想法.这位同学确定点C所用方法的依据是 .
 12. 如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 .
12. 如图,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,点O、A、B、C均在格点上,则过A、B、C三点的圆的圆心坐标为 . 13. 如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 .
13. 如图,CD是⊙O的直径,AB是弦,CD⊥AB,若OB=5,AB=8,则AC的长为 . 14. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.
14. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.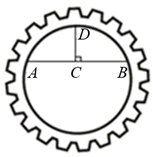 15. 如图,点 在半圆 上,BC是直径, .若 ,则BC的长为.
15. 如图,点 在半圆 上,BC是直径, .若 ,则BC的长为. 16. 如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长为
16. 如图,AB为⊙O的直径,弦CD⊥AB于点H,若AB=10,CD=8,则OH的长为
三、解答题
-
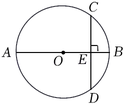
17. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=10,BE=2,求弦CD的长.
 18. 如图,是的弦,C是上的一点,且 , 于点E,交于点D.若的半径为6,求弦的长.
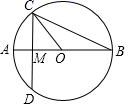
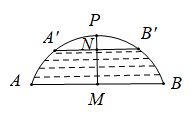
18. 如图,是的弦,C是上的一点,且 , 于点E,交于点D.若的半径为6,求弦的长. 19. 如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径.
19. 如图,M是CD的中点,EM⊥CD,若CD=4,EM=6,求所在圆的半径. 20. 如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF
20. 如图,AB、CD为⊙O的两条弦,AB∥CD,经过AB中点E的直径MN与CD交于F点,求证:CF=DF 21. 如图,在等腰三角形ABC中,AB=AC,AD⊥BC,垂足为D.
21. 如图,在等腰三角形ABC中,AB=AC,AD⊥BC,垂足为D. (1)、请用尺规作图作出三角形ABC的外接圆⊙O;(不写作法及证明,应保留作图痕迹)(2)、若BC=4,AD=5,求⊙O的半径r.
(1)、请用尺规作图作出三角形ABC的外接圆⊙O;(不写作法及证明,应保留作图痕迹)(2)、若BC=4,AD=5,求⊙O的半径r.