2022-2023初数北师大版八年级上册2.6实数同步练习

试卷更新日期：2022-07-23 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图1， $\sqrt{15}$ 在数轴对应的点可能是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
2. 下列说法正确的是（）

A、任何实数都有平方根 B、任何实数都立方根 C、数轴上的每一个点都表示一个有理数 D、两个无理数的和还是无理数

查看试题解析
3. 下列说法中，正确的是（）

A、不带根号的数都是有理数 B、两个无理数的和还是无理数 C、无理数就是开方开不尽的数 D、算术平方根等于它本身的数只有1和0

查看试题解析
4. 在 $R t Δ A B C$ 中， $∠ B = 90 °$ ， $A B = B C = 2$ ， $A C = a$ .下列关于a的四种说法：①a是无理数；②a可以用数轴上的一个点来表示；③a是8的算术平方根；④ $3 < a < 4$ .其中，所有正确的说法的序号是（）

A、①②④ B、②③④ C、①②③ D、①③④

查看试题解析
5. 如图所示，已知数轴上的点A、O、B、C、D分别表示数﹣2、0、1、2、3，则表示数3 $- \sqrt{5}$ 的点P应落在（）

A、线段AO上 B、线段OB上 C、线段BC上 D、线段CD上

查看试题解析
6. 如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{2}$ +1 C、1﹣ $\sqrt{2}$ D、﹣ $\sqrt{2}$

查看试题解析
7. 设P₁、P₂、P₃、P₄是不等于零的有理数，q₁、q₂、q₃、q₄是无理数，则下列四个数① $p_{1}^{2} + q_{1}^{2}$ ，②（P₂+q₂）² ， ③（P₃+q₃）q³ ， ④P₄（P₄+q₄）中必为无理数的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 下列说法正确的有（　　）
①实数和数轴上的点是一一对应的；

②一个数的算术平方根一定是正数

③负数没有立方根；

④16的平方根是±4，用式子表示是 $\sqrt{16}$ ＝±4；

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若AD＝AE，则数轴上点E所表示的数为(　　)

A、－ $\sqrt{5}$ B、1－ $\sqrt{5}$ C、 $\frac{- 1 - \sqrt{5}}{2}$ D、 $\frac{3}{2} - \sqrt{5}$

查看试题解析
10. 把无理数 $\sqrt{17}$ ， $\sqrt{11}$ ， $\sqrt{5}$ ，﹣ $\sqrt{3}$ 表示在数轴上，在这四个无理数中，被墨迹（如图所示）覆盖住的无理数是（）

A、 $\sqrt{17}$ B、 $\sqrt{11}$ C、 $\sqrt{5}$ D、﹣ $\sqrt{3}$

查看试题解析

二、填空题（共6题，共19分）

11. $\sqrt{49}$ 是（填写“有理数”或“无理数”）.

查看试题解析
12. 在数轴上表示 $- \sqrt{5}$ 的点与原点的距离等于.

查看试题解析
13. 在下列数中：①-0.32 ，②0.3 ，③- $\frac{π}{2}$ ，④ $\sqrt{7}$ ，⑤ $\frac{22}{7}$ ，⑥ $\sqrt{64}$ ，⑦- $\sqrt[3]{- 0.4}$ ， ⑧ $\sqrt{8}$ ，⑨1.203200320003（填序号）
有理数是：；无理数是；正数是；负数是．

查看试题解析
14. 如图，数轴上点A，B对应的实数分别是 $- 1$ ， 2，点C在线段AB上运动，如果点C表示无理数，那么点C可以是（写出一个即可）．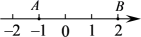

查看试题解析
15. 如图，在数轴上点A和点B之间表示整数的点共有个

查看试题解析
16. 如图．面积为8的正方形ABCD的顶点A在数轴上，点A表示实数 $- \sqrt{2}$ ，正方形ABCD绕点A旋转时，顶点B的运动轨迹与数轴的交点表示的数为

查看试题解析

三、解答题（共8题，共51分）

17. 在如图所示的数轴上画出表示 $\sqrt{5}$ 、 $2 \sqrt{2}$ 的点.（不写画法，保留画图痕迹）

查看试题解析
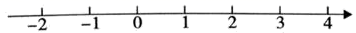18.
求出下列各数的相反数，在数轴上表示下列各数以及它们的相反数，并用“＜”连接：﹣ $\sqrt{2}$ ， $\frac{5}{2}$ ， 0， $\sqrt[3]{8}$ ．

查看试题解析
19. 把下列各数填入相应的集合内
5 ， $\sqrt{14}$ ，6 ， $\sqrt{\frac{9}{17}}$ ， $\frac{3}{2}$ ， $\sqrt[3]{8}$ ，-π ，-0.13

⑴有理数集合｛                                     ｝

⑵无理数集合｛                                     ｝

⑶正实数集合｛                                     ｝

⑷负实数集合｛                                     ｝

查看试题解析
20. 课堂上，老师让同学们从下列数中找一个无理数：
$- \frac{22}{7}$ ， $- \sqrt{2}$ ， $| - \frac{1}{2} |$ ，0， $2 π$ ， $- \sqrt[3]{8}$ ，

其中，甲说“ $- \frac{22}{7}$ ”，乙说“ $- \sqrt{2}$ ”，丙说“ $2 π$ ”

(1)、甲、乙、丙三个人中，说错的是．

(2)、请将老师所给的数字按要求填入下面相应的区域内；

查看试题解析
21. 如何将 $\sqrt{5}$ 用数轴上的点表示？关键是画出长为 $\sqrt{5}$ 的线段.方法1：因为 $5 = 1^{2} + 2^{2}$ ，所以我们可以通过画两条直角边分别为1、2的直角三角形来解决，我们把此法称为“和法”；方法2：因为 $5 = 3^{2} - 2^{2}$ ，所以我们可以通过画直角边为2，斜边为3的直角三角形来解决，我们把此法称为“差法”.

(1)、用“差法”将 $\sqrt{3}$ 用数轴上的点表示（注：需用尺规作图，保留作图痕迹，不写画法）

(2)、对于正整数n，猜想当n是什么数时，我们都能通过“差法”，将 $\sqrt{n}$ 用数轴上的点表示，并证明你的猜想.

查看试题解析
22. 我们在学习第二章《实数》这节课时，画了如图所示的图形，即“以数轴上单位长度为1的线段为边作一个正方形，然后以原点O为圆心， $O B$ 的长为半径作弧，交数轴的正半轴于点A”，请解答下列问题：

(1)、线段 $O A$ 的长度是多少？

(2)、这个图形的目的是为了说明什么？

(3)、请在数轴上画出表示 $- \sqrt{10}$ 的点P.（不写作法，保留作图痕迹）

查看试题解析
23. 如图1，这是一个由27个同样大小的立方体组成的三阶魔方，体积为27．

(1)、求出这个魔方的棱长．

(2)、图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长．

(3)、如图2，把图1中的正方形ABCD放到数轴上，使得点A与−1重合，那么点D在数轴上表示的数为．

查看试题解析

2022-2023初数北师大版八年级上册2.6实数 同步练习

一、单选题（每题3分，共30分）

二、填空题（共6题，共19分）

三、解答题（共8题，共51分）

2022-2023初数北师大版八年级上册2.6实数同步练习