2022-2023初数北师大版八年级上册2.4估算同步练习

试卷更新日期：2022-07-23 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列整数中，与 $\sqrt{10}$ －1最接近的是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 无理数 $\sqrt{5}$ 的整数部分是（　　）

A、4 B、3 C、2 D、1

查看试题解析
3. 估计 $\sqrt{18}$ 的值在（）

A、 $1$ 和 $2$ 之间 B、 $2$ 和 $3$ 之间 C、 $3$ 和 $4$ 之间 D、 $4$ 和 $5$ 之间

查看试题解析
4. 若 $\sqrt{5}$ 的整数部分为a，小数部分为b，则 $2 a + b$ 等于（）

A、 $\sqrt{5} + 1$ B、 $\sqrt{5} - 1$ C、 $\sqrt{5} + 2$ D、 $\sqrt{5} - 2$

查看试题解析
5. 如图1，在 $△ A B C$ 中， $A B = B C = 2$ ， $∠ B = 120 °$ ， M是 $B C$ 的中点，设 $A M = a$ ，则表示实数a的点落在数轴上（如图2）所标四段中的（）

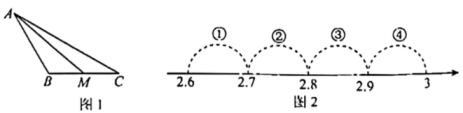A、①段 B、②段 C、③段 D、④段

查看试题解析
6. 数轴上A ， B ， C ， D四点中，两点之间的距离最接近于 $\sqrt{6}$ 的是（　　）

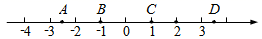A、点C和点D B、点B和点C C、点A和点C D、点A和点B

查看试题解析
7. 若a＜ $\sqrt{7}$ ＜b ，且a与b为连续整数，则a与b的值分别为（　　）

A、1；2 B、2；3 C、3；4 D、4；5

查看试题解析
8. 估计 $\sqrt{13} - 1$ 的值在（）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
9. 已知44²＝1936，45²＝2025，46²＝2116，47²＝2209，若n为整数且n＜ $\sqrt{2170}$ ＜n＋1，则n的值为（）

A、44 B、45 C、46 D、47

查看试题解析
10. 已知 $\sqrt[3]{326} \approx 6.882$ ，若 $\sqrt[3]{x} \approx 68.82$ ，则x的值约为（）

A、326000 B、32600 C、3.26 D、0.326

查看试题解析

二、填空题（每空2分，共20分）

11. 若 $a < \sqrt{11} < b$ ，且a，b是两个连续的整数，则 $a + b$ 的值为．

查看试题解析
12. 与 $\sqrt{26}$ 最接近的整数为.

查看试题解析
13. 3+ $\sqrt{3}$ 的整数部分是a，3－ $\sqrt{3}$ 的小数部分是b，则a+b等于.

查看试题解析
14. 已知43²＝1849，44²＝1936，45²＝2025，46²＝2116，若n为整数且n＜ $\sqrt{2022}$ ＜n＋1，则n的值是．

查看试题解析
15. 已知 $a$ 是 $- 8$ 的立方根， $b$ 是 $1 \frac{7}{9}$ 的算术平方根， $c$ 是 $\sqrt{11}$ 的整数部分， $d$ 与 $- \sqrt{2}$ 互为相反数．

(1)、 $a =$ ， $b =$ ， $c =$ ， $d =$ ；

(2)、将 $a$ 、 $b$ 、 $c$ 、 $d$ 用“＜”按从小到大的顺序排列起来．

查看试题解析
16. 设[x]表示最接近x的整数（x≠n+0.5，n为整数），则 $[\sqrt{1}] + [\sqrt{2}] + [\sqrt{3}] + \dots + [\sqrt{20}]$ =

查看试题解析

三、解答题（共8题，共50分）

17. 已知 $2 a - 1$ 的算术平方根是3， $3 a + b - 1$ 的算术平方根是4，c是 $\sqrt{30}$ 的整数部分，求 $a + 32 b - c$ 的立方根.

查看试题解析
18. 阅读理解：
$∵ \sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ， $∴ 1 < \sqrt{5} - 1 < 2$ .

$∴ \sqrt{5} - 1$ 的整数部分为1.

$∴ \sqrt{5} - 1$ 的小数部分为 $(\sqrt{5} - 1) - 1 = \sqrt{5} - 2$

解决问题：已知a是 $\sqrt{19} - 3$ 的整数部分，b是 $\sqrt{26} - 2$ 的小数部分，求 ${(- a)}^{3} + {(b + 5)}^{2}$ 的平方根.

查看试题解析
19. $5 + \sqrt{11}$ 的小数部分为 $a$ ， $5 - \sqrt{11}$ 的小数部分为 $b$ ，求：

(1)、a+b的值．

(2)、a-b的值．

(3)、 $a \cdot b$ 的值．

查看试题解析
20. 已知x是 $\sqrt{10}$ 的整数部分,y是 $\sqrt{10}$ 的小数部分,求 ${(y - \sqrt{10})}^{x - 1}$ 的平方根.

查看试题解析
21. 大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数．因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小燕用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分．理由是：对于正无理数，用本身减去其整数部分，差就是其小数部分．因为 $\sqrt{2}$ 的整数部分为1，所以 $\sqrt{2}$ 的小数部分为 $\sqrt{2} - 1$ ．
参考小燕同学的做法，解答下列问题：

(1)、写出 $\sqrt{13}$ 的小数部分为；

(2)、已知 $7 + \sqrt{7}$ 与 $7 - \sqrt{7}$ 的小数部分分别为a和b，求a²＋2ab＋b²的值；

(3)、如果 $\sqrt{9} + \sqrt[3]{9} = x + y$ ，其中x是整数，0＜y＜1，那么 $\frac{2}{5} x + y$ ＝

(4)、设无理数 $\sqrt{m}$ （m为正整数）的整数部分为n，那么 $m - \sqrt{m}$ 的小数部分为（用含m，n的式子表示）．

查看试题解析
22. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确.

信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5﹣2得来的；

信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2＜ $\sqrt{5}$ ＜3，是因为 $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ：根据上述信息，回答下列问题：

(1)、 $\sqrt{13}$ 的整数部分是，小数部分是.

(2)、10+ $\sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为a＜10+ $\sqrt{3}$ ＜b则a+b＝.

(3)、若 $\sqrt{30}$ ﹣3＝x+y，其中x是整数，且0＜y＜1，请求x﹣y的相反数.

查看试题解析
23. 已知2a+3的立方根是3，a+b﹣1的算术平方根是4，c是 $\sqrt{11}$ 的整数部分.

(1)、求a，b，c的值.

(2)、求a﹣4b+3c的平方根.

查看试题解析
24. 数学家华罗庚在一次出国访问途中，看到飞机上的乘客阅读的杂志上有道智力题，求59319的立方根，华罗庚脱口而出“39”，邻座的乘客十分惊奇，忙问其中的奥妙.你知道怎样迅速的计算结果吗？请你按下面的结果试一试.
第一步： $∵ \sqrt[3]{1000} = 10$ ， $\sqrt[3]{1000000} = 100$
$1000 < 59319 < 1000000$ ， $∴ 10 < \sqrt[3]{59319} < 100$
它的立方根是一个两位数.
第二步： $∵ 59319$ 的个位数是9， $9^{3} = 729$ .
$∴$ 能确定 $\sqrt{59319}$ 的个位数是9.
第三步：如果划出59319后面的三位数，得到数59
而 $\sqrt[3]{27} < \sqrt[3]{59} < \sqrt[3]{64}$ ，可得 $30 < \sqrt[3]{59319} < 40$ .
由此确定59319的立方根的十位数是3， $∴$ 它的立方根是39.
[解答问题]
根据上面的材料解答下面的问题：

(1)、求110592的立方根，写出步骤.

(2)、填空： $\sqrt[3]{85184} =$ .

查看试题解析

2022-2023初数北师大版八年级上册2.4估算 同步练习

一、单选题（每题3分，共30分）

二、填空题（每空2分，共20分）

三、解答题（共8题，共50分）

2022-2023初数北师大版八年级上册2.4估算同步练习