2022-2023初数北师大版八年级上册第一章勾股定理章末检测

试卷更新日期：2022-07-23 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，如果 $A B = 8$ ， $B C = 6$ ，那么 $A C$ 的长是（）．

A、10 B、 $2 \sqrt{7}$ C、10或 $2 \sqrt{7}$ D、7

查看试题解析
2. 直角三角形的两直角边长分别为5和12，则斜边长为（）

A、13 B、14 C、 $\sqrt{89}$ D、1

查看试题解析
3. 如图，在Rt $△$ ABC中，∠B＝90°，AB＝3，BC＝4，将 $△$ ABC折叠，使点B恰好落在边AC上，与点 $B$ 重合，AE为折痕，则E $B$ 长为（）

A、3cm B、2.5cm C、1.5cm D、1cm

查看试题解析
4. 如图，点A，B都在格点上，若 $B C= \frac{2 \sqrt{13}}{3}$ ，则 $A C$ 的长为（）

A、 $\sqrt{13}$ B、 $\frac{4 \sqrt{13}}{3}$ C、 $2 \sqrt{13}$ D、 $3 \sqrt{13}$

查看试题解析
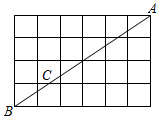5. 下列各组数中，以它们为边长的线段能构成直角三角形的是（）

A、1，2，3 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、4，5，6 D、12，15，20

查看试题解析
6. 已知△ABC中，∠A、∠B、∠C所对的边分别是a、b、c，满足下列条件的三角形中，不能判定△ABC为直角三角形是的（）

A、∠A：∠B：∠C＝3：4：5 B、∠A＝∠C﹣∠B C、a：b：c＝5：12：13 D、∠A：∠B：∠C＝1：2：3

查看试题解析
7. 在如图所示的方格纸中，点A，B，C均为格点，则 $∠ A B C$ 的度数是（）

A、 $30 °$ B、 $35 °$ C、 $45 °$ D、 $60 °$

查看试题解析
8. 在下列条件：①∠A+∠B＝∠C，②∠A：∠B：∠C＝3：4：5，③∠C＝∠A﹣∠B，④a：b：c＝3：4：5中，能确定△ABC是直角三角形的条件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图有一个水池，水面BE的宽为16尺，在水池的中央有一根芦苇，它高出水面2尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，则这个芦苇的高度是（）

A、26尺 B、24尺 C、17尺 D、15尺

查看试题解析
10. 勾股定理是人类最伟大的科学发明之一．如图1，以直角三角形ABC的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内，三个阴影部分面积分别记为S₁ ， S₂ ， S₃ ，若已知S₁＝2，S₂＝5，S₃＝8，则两个较小正方形纸片的重叠部分（四边形DEFG）的面积为（）

A、7 B、10 C、13 D、15

查看试题解析

二、填空题（每题4分，共24分）

11. △ABC中，AB＝ $6 \sqrt{10}$ ， AC＝10，BC边上的高AD＝6，则BC边长为．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 13$ ， $B C = 12$ ， D为 $B C$ 边上一点，将 $△ A B D$ 沿 $A D$ 折叠，若点B恰好落在线段 $A C$ 的延长线上的点E处，则 $D E$ 的长为.

查看试题解析
13. 定义：在平面直角坐标系中，把从点P出发沿横或纵方向到达点Q（至多拐一次弯）的路径长称为P，Q的“实际距离”.如图，若 $P (- 1 ， 1)$ ， $Q (2 ， 3)$ ，则P，Q的“实际距离”为5，即 $P S + S Q = 5$ 或 $P T + T Q = 5$ .环保低碳的公共自行车，逐渐成为市民出行喜欢的交通工具.设A，B，C三个小区的坐标分别为 $A (- 3 ， - 1)$ ， $B (- 5 ， 3)$ ， $C (1 ， 5)$ ，若点M表示公共自行车停放点，且满足M到A，B，C的“实际距离”相等，则点M的坐标是.

查看试题解析
14. 如图所示的网格是正方形网格，∠APB＝°．

查看试题解析
15. 如今人们锻炼身体的意识日渐增强，但是发现少数人保护环境的意识仍显淡薄，应提醒注意．下图是房山某公园的一角，有人为了抄近道而避开路的拐角 $∠ A B C$ （ $∠ A B C = 90 °$ ），于是在草坪内走出了一条不该有的“捷径路AC” ．已知 $A B = 30$ 米， $B C = 40$ 米，他们踩坏了米的草坪，只为少走米的路．

查看试题解析
16. 如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开，若测得 $A C = 3 km$ ， $B C = 4 km$ ，则M，C两点间的距离为km.

查看试题解析

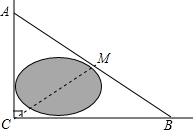
三、解答题（共8题，共66分）

17. 如图，在Rt△ABC中，∠B=90°，AB=4，BC=3，阴影部分是一个长方形，AE=1，求阴影部分的面积．

查看试题解析
18. 如图， $A B = 3$ ， $C B = 4$ ， $∠ A B C = 90 °$ ， $C D = 13$ ， $A D = 12$ .求该图形的面积.

查看试题解析
19. 如图是一面长方形彩旗完全展平时的尺寸图（单位：cm）．其中长方形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为长方形绸缎旗面，将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220cm.在无风的天气里，彩旗自然下垂．求彩旗下垂时最低处离地面的最小高度h.

查看试题解析
20. 在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， C B = C A = 2 \sqrt{2}$ ，点D是线段 $A B$ 上一点，连接 $C D$ ，在 $C D$ 右侧作 $∠ D C E = 90 °$ ，且 $C E = C D$ ，连接 $A E$ ，已知 $A E = 1$ ．

(1)、求 $∠ C A E$ 的度数；

(2)、求 $C D$ 的长；

查看试题解析
21. 如图，在 $△$ ABC中，AB＝10cm，AC＝8cm，BC＝6cm．现将 $△$ ABC进行折叠，使点A恰好与点B重合．

(1)、判断 $△$ ABC的形状，并说明理由；

(2)、求折痕DE的长．

查看试题解析
22. 小王与小林进行遥控赛车游戏，终点为点A，小王的赛车从点C出发，以 $4$ 米/秒的速度由西向东行驶，同时小林的赛车从点B出发，以 $3$ 米/秒的速度由南向北行驶（如图）.已知赛车之间的距离小于或等于 $25$ 米时，遥控信号会产生相互干扰， $A C = 40$ 米， $A B = 30$ 米，

(1)、出发 $3$ 秒钟时，遥控信号是否会产生相互干扰？

(2)、当两赛车距A点的距离之和为 $35$ 米时，遥控信号是否会产生相互干扰？

查看试题解析
23. 如图所示，一架梯子AB斜靠在墙面上，且AB的长为2.5米．

(1)、若梯子底端离墙角的距离OB为1.5米，求这个梯子的顶端A距地面有多高？

(2)、在（1）的条件下，如果梯子的顶端A下滑0.5米到点A'，那么梯子的底端B在水平方向滑动的距离BB'为多少米？

查看试题解析
24. 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．

(1)、特例感知
等腰直角三角形勾股高三角形（请填写“是”或者“不是”）；

(2)、如图1，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高．若 $B D = 2 A D = 2$ ，试求线段CD的长度．

(3)、深入探究
如图2，已知△ABC为勾股高三角形，其中C为勾股顶点且CA＞CB ， CD是AB边上的高．试探究线段AD与CB的数量关系，并给予证明；

(4)、推广应用
如图3，等腰△ABC为勾股高三角形，其中 $A B = A C > B C$ ，CD为AB边上的高，过点D向BC边引平行线与AC边交于点E ．若 $C E = a$ ，试求线段DE的长度．

查看试题解析

2022-2023初数北师大版八年级上册第一章勾股定理 章末检测

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2022-2023初数北师大版八年级上册第一章勾股定理章末检测