（人教版）2022-2023学年度第一学期九年级数学第24章 圆 单元测试
试卷更新日期：2022-07-22 类型：单元试卷
一、单选题
-
1. 如图，A，B，C是某社区的三栋楼，若在AC中点D处建一个5G基站，其覆盖半径为300 m，则这三栋楼中在该5G基站覆盖范围内的是（ ）
A、A，B，C都不在 B、只有B C、只有A，C D、A，B，C2. 如图，AB 为⊙O 的直径，弦 CDAB，垂足为点 E，若 ⊙O的半径为5，CD=8，则AE的长为（ ）
A、3 B、2 C、1 D、3. 如图，在半径为5的圆O中，AB，CD是互相垂直的两条弦，垂足为P，且AB=CD=6，则OP的长为（ ）
A、3 B、4 C、 D、4. 如图，△ABC内接于圆O，AC＝10，BC＝24，且∠A＝90°+∠B，则点O到AB的距离为（ ）
A、 B、 C、2.4 D、5. 如图，△ABC的外接圆半径为8，∠ACB＝60°，则AB的长为（ ）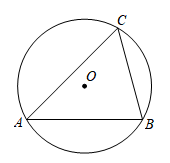
A、8 B、4 C、6 D、46. 已知⊙的半径为 ， 点到圆心的距离为 ， 那么点与⊙的位置关系是（ ）．A、点在⊙外 B、点在⊙内 C、点在⊙上 D、无法确定7. 如图，AB是⊙O直径，过⊙O上的点C作⊙O切线，交AB的延长线于点D，若∠D＝40°，则∠A大小是（ ）
A、20° B、25° C、30° D、35°8. 如图，正六边形螺帽的边长是4cm，那么这个正六边形半径R和扳手的开口a的值分别是（ ）
A、2，2 B、4，4 C、4，2 D、4，9. 如图，在中，以边的中点D为圆心，长为半径画弧，交于E点，若 ， 则扇形的面积为（ ）
A、 B、 C、 D、10. 在中， ， ， ． 把绕点A顺时针旋转后，得到 ， 如图所示，则点B所走过的路径长为（ ）
A、 B、 C、 D、二、填空题
-
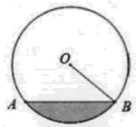
11. 一根排水管的截面如图所示，已知排水管的半径 ， 水面宽 ， 如果再注入一些水，当水面AB的宽变为16时，则水面AB上升的高度为.
12. 如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连接OB、OC，若弦BC的长度为 ，则∠BAC＝度.
13. 如图为半圆的直径， ， 点P为半圆的三等分点，点D为弧上一动点，作.连接交于点N，则的最小值为.
14. 《九章算术》是我国古代的数学名著，书中有这样的一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”．其意思是：“如图，现有直角三角形，勾（短直角边）长为 8 步，股（长直角边）长为 15 步，问该直角三角形所能容纳的最大圆的直径是多少？”答：该直角三角形所能容纳的最大圆的直径是步．
15. 已知扇形的圆心角为120°，它所对弧长为20πcm，则扇形的半径为 ．三、解答题
-
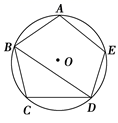
16. 已知：如图， 、 为 的半径，C、D分别为 、 的中点，求证： .
17. 如图，AB为⊙O的弦，OC⊥AB于点M，交⊙O于点C．若⊙O的半径为10，OM：MC＝3：2，求AB的长．
18. 如图，弧 弧 求证： ．
19. 如图，是的外接圆⊙O的直径，若∠ACB=50°，求∠BAD的度数．
20. 如图，AB、AC是⊙O的两条弦，且AB=AC．求证：∠1=∠2．
21. 如图，在⊙O中，AB为直径，BP为⊙O的弦，AC与BP的延长线交于点C，且 ， 于点E，求证：PE是⊙O的切线．
