(人教版)2022-2023学年度第一学期九年级数学24.3 正多边形和圆 同步测试
试卷更新日期:2022-07-22 类型:同步测试
一、单选题
-
1. 已知一个正多边形的内角是140°,则它是几边形( )A、10 B、9 C、8 D、72. 如图,若正六边形
 绕着中心 旋转角 得到的图形与原来的图形重合,则 最小值为( )
绕着中心 旋转角 得到的图形与原来的图形重合,则 最小值为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,是半圆的直径,、是半圆上的两点, , 则( )
3. 如图,是半圆的直径,、是半圆上的两点, , 则( )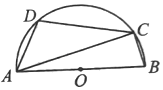 A、55° B、65° C、75° D、85°4. 如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是 ( )
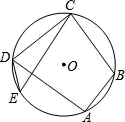
A、55° B、65° C、75° D、85°4. 如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是 ( )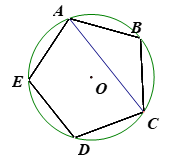 A、72° B、70° C、60° D、45°5. 如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )A、
A、72° B、70° C、60° D、45°5. 如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )A、 B、
B、 C、
C、 D、
D、 6. ⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )A、2 B、 C、2 D、27. 如图,正六边形ABCDEF的半径 , 则点B的坐标为( )
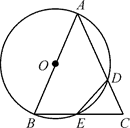
6. ⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )A、2 B、 C、2 D、27. 如图,正六边形ABCDEF的半径 , 则点B的坐标为( ) A、 B、 C、 D、8. 如图,AE是四边形ABCD外接圆的直径, , , 则的度数为( )
A、 B、 C、 D、8. 如图,AE是四边形ABCD外接圆的直径, , , 则的度数为( )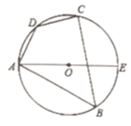 A、50° B、55° C、60° D、65°9. 如图,D是等边△ABC外接圆 上的点,且∠CAD=20°,则∠ACD的度数为( )
A、50° B、55° C、60° D、65°9. 如图,D是等边△ABC外接圆 上的点,且∠CAD=20°,则∠ACD的度数为( ) A、20° B、30° C、40° D、45°10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、20° B、30° C、40° D、45°10. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )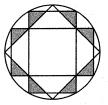 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 如图,在⊙O中,AB是⊙O的内接正六边形的一边,BC是⊙O的内接正十边形的一边,则∠ABC=°.
 12. 如图,在圆内接正六边形ABCDEF中,半径OA=4,则这个正六边形的边长为 .
12. 如图,在圆内接正六边形ABCDEF中,半径OA=4,则这个正六边形的边长为 . 13. 如图,PA,PB分别切于点A,B, , 若点C在上,且不与A,B重合,则的度数是 .
13. 如图,PA,PB分别切于点A,B, , 若点C在上,且不与A,B重合,则的度数是 . 14. 如图,把分成相等的六段弧,依次连接各分点得到正六边形ABCDEF,如果的周长为 , 那么该正六边形的边长是 .
14. 如图,把分成相等的六段弧,依次连接各分点得到正六边形ABCDEF,如果的周长为 , 那么该正六边形的边长是 .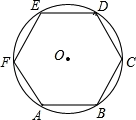 15. 如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A= °
15. 如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A= °
三、解答题
-
16. 已知圆内接正十二边形的面积为S,求同圆的内接正六边形的面积.
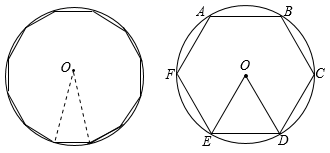 17. 如图,四边形 内接于 ,若 ,求 的大小.
17. 如图,四边形 内接于 ,若 ,求 的大小. 18. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.
18. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.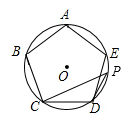 19. 根据图中所给信息,解出下图中未知数 、 的值.
19. 根据图中所给信息,解出下图中未知数 、 的值. 20. 如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
20. 如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .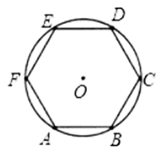 21. 已知如图,AB是⊙O的直径,C、D是圆上的两点,且 ,若 ,求 的度数.
21. 已知如图,AB是⊙O的直径,C、D是圆上的两点,且 ,若 ,求 的度数.