（人教版）2022-2023学年度第一学期九年级数学24.2.1 点和圆的位置关系 同步测试
试卷更新日期：2022-07-22 类型：同步测试
一、单选题
-
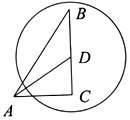
1. 如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝7，点D在边BC上，CD＝3，以点D为圆心作⊙D，其半径长为r，要使点A恰在⊙D外，点B在⊙D内，那么r的取值范围是（ ）
A、4＜r＜5 B、3＜r＜4 C、3＜r＜5 D、1＜r＜72. 已知⊙O半径为4，圆心O在坐标原点上，点P的坐标为（3，4），则点P与⊙O的位置关系是（ ）A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不能确定3. 已知⊙O的直径为4，若 ， 则点与⊙O的位置关系是（ ）A、点在⊙O上 B、点在⊙O内 C、点在⊙O外 D、无法判断4. 已知点P到圆心O的距离为5，若点P在圆内，则的半径可能为（ ）A、3 B、4 C、5 D、65. 如图，△ABC为锐角三角形，BC=6，∠A=45°，点O为△ABC的重心，D为BC中点，若固定边BC，使顶点A在△ABC所在平面内进行运动，在运动过程中，保持∠A的大小不变，则线段OD的长度的取值范围为（ ）
A、 B、 C、 D、6. 如图，在矩形 中， ， .若以点B为圆心，以4cm长为半径作OB，则下列选项中的各点在 外的是（ ）
A、点A B、点B C、点C D、点D7. 如图， 中， 于点D，点P为 上的点，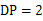
，以点P为圆心 为半径画圆，下列说法错误的是（ ）
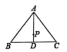A、点A在 外 B、点B在 外 C、点C在 外 D、点D在 内8. 如图，在平面直角坐标系xOy中，点A（0，3），点B（2，1），点C（2，－3）．则经画图操作可知：△ABC的外接圆的圆心坐标是（ ）
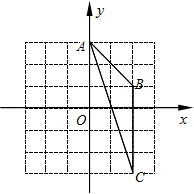A、（－2，－1） B、（－1，0） C、（－1，－1） D、（0，－1）9. 在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法错误的是（ ）A、当a＜5时，点B在⊙A内 B、当1＜a＜5时，点B在⊙A内 C、当a＜1时，点B在⊙A外 D、当a＞5时，点B在⊙A外10. 如图所示的正方形网格中，A，B，C三点均在格点上，那么ABC的外接圆圆心是（ ）
A、点E B、点F C、点G D、点H二、填空题
-
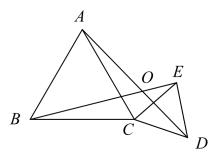
11. 如图，和都是等边三角形， ， ， 固定 ， 把绕点C旋转任意角度，连接AD，BE，设AD，BE所在的直线交于点O，则在旋转过程中，始终有 ， 且的大小保持不变，这时点O到直线AB的最大距离为 ．
12. 边长为2的正三角形的外接圆的半径等于 ．13. 如图，在平面直角坐标系中，点A，B，C的横、纵坐标都为整数，过这三个点作一条圆弧，则此圆弧的圆心坐标为 ．
14. ⊙O内一点P到⊙O上的最近点的距离为1，最远点的距离为7，则⊙O的半径为 ．15. 如图，O是的外心，且∠ABC=40°，∠ACB=70°，则 ．
三、解答题
-
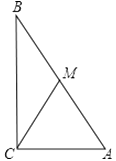
16. 已知⊙O的半径为2，点P到圆心O的距离OP=m，且m使关于x的方程 有实数根，求点P与⊙O的位置关系.17. 已知：如图，△ABC中， ， cm， cm，CM是中线，以C为圆心，以 cm长为半径画圆，则点A、B、M与⊙C的关系如何？
18. 如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP=4，求线段OM的最小值．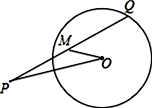
19. 如图，在 中， ， 是线段 的中点，以 为直径作 ，试判断点 与 的位置关系．
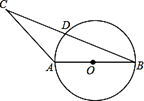20. 如图，要把残破的轮片复制完整，已知弧上的三点A、B、C.
①用尺规作图法找出
所在圆的圆心(保留作图痕迹，不写作法)；②设△ABC是等腰三角形，底边BC＝8cm，腰AB＝5cm，求圆片的半径R.
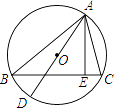
21.如图，AD为△ABC的外接圆O的直径，AE⊥BC于E．求证：∠BAD=∠EAC．
22.如图，等边△ABC内接于⊙O，P是弧AB上任一点（点P不与A、B重合），连AP，BP，过C作CM∥BP交PA的延长线于点M，
（1）求证：△PCM为等边三角形；
（2）若PA=1，PB=2，求梯形PBCM的面积．
