辽宁省大连市2021-2022学年高一上学期数学期末考试试卷

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | - 1 \leq x \leq 4}$ ， $B = {x | - 2 \leq x \leq 3}$ ，则 $A ∩ B =$ （）

A、 $[- 1 ， 3]$ B、 $[- 2 ， 4]$ C、 $[- 2 ， - 1]$ D、 $[- 1 ， 4]$

查看试题解析
2. 以下数据为参加数学竞赛决赛的15人的成绩：56，70，72，78，79，80，81，83，84，86，88，90，91，94，98，则这15人成绩的70%分位数是（）

A、86 B、87 C、88 D、89

查看试题解析
3. 已知函数 $y = f (x)$ 在区间 $[a ， b]$ 上的图像是连续不断的，则“ $f (a) f (b) < 0$ ”是“函数 $y = f (x)$ 在区间 $[a ， b]$ 内有零点”（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 在 $△ A B C$ 中， $P$ ， $Q$ 分别是边 $A B$ ， $A C$ 上的点，且 $\vec{A P} = \frac{1}{3} \vec{A B}$ ， $\vec{B Q} = \frac{1}{3} \vec{B C}$ ，若 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，则 $\vec{P Q} =$ （）

A、 $\frac{1}{3} \vec{a} + \frac{1}{3} \vec{b}$ B、 $- \frac{1}{3} \vec{a} + \frac{1}{3} \vec{b}$ C、 $\frac{1}{3} \vec{a} - \frac{1}{3} \vec{b}$ D、 $- \frac{1}{3} \vec{a} - \frac{1}{3} \vec{b}$

查看试题解析
5. 我国古代数学名著《九章算术》中有以下问题：“今有人合伙买羊，每人出5钱，差45钱；每人出7钱，差3钱.问合伙人数､羊价各是多少.”由此可推算，羊价为（）

A、24钱 B、165钱 C、21钱 D、150钱

查看试题解析
6. 抛掷一枚质地均匀且各个面上分别表以数字1，2，3，4，5，6的正方体玩具.设事件A为“向上一面点数为偶数”，事件B为“向上一面点数为6的约数”，则 $P (A + B)$ 为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
7. 神舟十二号载人飞船搭载3名宇航员进入太空，在中国空间站完成了为期三个月的太空驻留任务，期间进行了很多空间实验，目前已经顺利返回地球．在太空中水资源有限，要通过回收水的方法制造可用水．回收水是将宇航员的尿液、汗液和太空中的水收集起来经过特殊的净水器处理成饮用水，循环使用．净化水的过程中，每增加一次过滤可减少水中杂质20%，要使水中杂质减少到原来的5%以下，则至少需要过滤的次数为（）（参考数据 $l g 2 = 0.3010$ ）

A、10 B、12 C、14 D、16

查看试题解析
8. 已知幂函数 $y = x^{a}$ 与 $y = x^{b}$ 的部分图像如图所示，直线 $x = m^{2}$ ， $x = m (0 < m < 1)$ 与 $y = x^{a}$ ， $y = x^{b}$ 的图像分别交于A，B，C，D四点，且 $| A B | = | C D |$ ，则 $m^{a} + m^{b} =$ （）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析

二、多选题

9. 若 $a b > 0$ ，则下列不等式中恒成立的有（）

A、 $a^{2} + b^{2} \geq 2 a b$ B、 $a + b \geq 2 \sqrt{a b}$ C、 $(a + \frac{1}{a}) (b + \frac{1}{b}) \geq 4$ D、 $\frac{b}{a} + \frac{a}{b} \geq 2$

查看试题解析
10. 下列说法不正确的是（）

A、若A，B为两个事件，则“A与B互斥”是“A与B相互对立”的必要不充分条件 B、若A，B为两个事件，则 $P (A + B) = P (A) + P (B)$ C、若事件A，B，C两两互斥，则 $P (A) + P (B) + P (C) = 1$ D、若事件A，B满足 $P (A) + P (B) = 1$ ，则A与B相互对立

查看试题解析
11. 如果 ${\vec{e}}_{1} ， {\vec{e}}_{2}$ 是平面α内两个不共线的向量，那么下列说法中不正确的是（）

A、 $λ {\vec{e}}_{1} + μ {\vec{e}}_{2}$ (λ，μ∈R)可以表示平面α内的所有向量 B、对于平面α内任一向量 $\vec{a}$ ，使 $\vec{a} = λ {\vec{e}}_{1} + μ {\vec{e}}_{2}$ 的实数对(λ，μ)有无穷多个 C、若向量 $λ_{1} {\vec{e}}_{1} + μ_{1} {\vec{e}}_{2}$ 与 $λ_{2} {\vec{e}}_{1} + μ_{2} {\vec{e}}_{2}$ 共线，则有且只有一个实数λ，使得 $λ_{1} {\vec{e}}_{1} + μ_{1} {\vec{e}}_{2} = λ (λ_{2} {\vec{e}}_{1} + μ_{2} {\vec{e}}_{2})$ D、若实数λ，μ使得 $λ {\vec{e}}_{1} + μ {\vec{e}}_{2} = 0$ ，则λ=μ=0

查看试题解析
12. 高斯是德国著名的数学家，近代数学奠基者之一.用其名字命名的高斯取整函数为 $y = [x]$ ， $[x]$ 表示不超过x的最大整数.例如： $[- 3.5] = - 4$ ， $[2.1] = 2$ .已知函数 $f (x) = \frac{e^{x}}{1 + e^{x}} - \frac{1}{2}$ ， $g (x) = [f (x)]$ ，则下列说法中正确的是（）

A、 $f (x)$ 是偶函数 B、 $f (x)$ 在R上是增函数 C、 $g (x)$ 是偶函数 D、 $g (x)$ 的值域是 ${- 1 ， 0}$

查看试题解析

三、填空题

13. 某校学生高一年级有400人，高二年级有300人，高三年级有200人，现用分层抽样的方法从所有学生中抽取一个容量为 $n$ 的样本．已知从高三学生中抽取的人数为10，那么 $n$ = ．

查看试题解析
14. 已知函数 $f (x) = a^{x} + b$ （ $a > 0$ 且 $a \neq 1$ ）的图像过点 $(1 ， 7)$ ，其反函数 $y = f^{- 1} (x)$ 的图像过点 $(4 ， 0)$ ，则 $a$ 的值为.

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $P$ 为 $D C$ 边上的动点，设向量 $\overset{⇀}{A C} = λ \overset{⇀}{D B} + μ \overset{⇀}{A P}$ ，则 $λ + μ$ 的最大值为．

查看试题解析
16. 已知 $f (x) = {\begin{array}{l} | x + 2 | ， x \leq 0 \\ | l o g_{3} x | ， x > 0 \end{array}$ ，若方程 $f (x) - a = 0$ 有四个根 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 且 $x_{1} < x_{2} < x_{3} < x_{4}$ ，则 $x_{1} + x_{2} + x_{3} + x_{4}$ 的取值范围是.

查看试题解析

四、解答题

17. 已知不等式 $| x - 4 | \leq 2$ 的解集为 $A$ ，当 $m > 0$ 时，关于 $x$ 的不等式 $x^{2} - 4 x - m^{2} + 4 \leq 0$ 的解集为 $B$ .

(1)、求 $A$ 、 $B$ ；

(2)、当 $m > 4$ 时，求证： $x \in A$ 是 $x \in B$ 的充分条件.

查看试题解析
18.

(1)、已知 $A (3 ， - 6)$ ， $B (- 5 ， 2)$ ， $C (6 ， y)$ 三点共线，求 $y$ 的值；

(2)、在（1）的条件下求线段 $A C$ 的两个三等分点的坐标.

查看试题解析
19. 从某学校随机抽取100名学生，测得他们的身高（单位：cm），按照区间 $[160 ， 165)$ ， $[165 ， 170)$ ， $[170 ， 175)$ ， $[175 ， 180)$ ， $[180 ， 185]$ 分组，得到样本身高的频率分布直方图，如图所示.

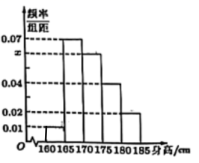(1)、求频率分布直方图中x的值；

(2)、估计该校学生身高的平均数（每组数据以区间中点值为代表）；

(3)、估计该校学生身高的75%分位数.

查看试题解析
20. 已知函数 $g (x) = a^{x - 1} - 1$ （a是常数， $a > 0$ 且 $a \neq 1$ ）的图像过定点 $(m ， n)$ ，函数 $f (x) = m x + \frac{4}{x} + n$ .

(1)、求证：函数 $f (x)$ 在 $[2 ， + \infty)$ 上单调递增；

(2)、解不等式 $f (x^{2} - 2 x + 4) + f (- 7) \leq 0$ .

查看试题解析
21. 甲､乙､丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终胜利，比赛结束.经抽签，甲､乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为 $\frac{1}{2}$ .

(1)、求比赛四场结束且丙获胜的概率；

(2)、求甲最终获胜的概率.

查看试题解析
22. 已知函数 $f (x) = \log_{a} (x - \frac{a}{2}) + \log_{a} (x - a)$ （ $a > 0$ 且 $a \neq 1$ ）．

(1)、当 $a = 2$ 时，解不等式 $f (x) > 1$ ；

(2)、 $\forall x \in [2 a ， 4 a]$ ， $f (x) \leq 1$ ，求实数 $a$ 的取值范围；

(3)、在（2）的条件下，是否存在 $α ， β \in (a ， + \infty)$ ，使 $f (x)$ 在区间 $[α ， β]$ 上的值域是 $[\log_{a} β ， \log_{a} α]$ ？若存在，求实数 $a$ 的取值范围；若不存在，试说明理由．

查看试题解析