广东省东莞市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x > - 1$ B、 $x \geq 1$ C、 $x \geq 2$ D、 $x < 3$

查看试题解析
2. 若一个直角三角形的两直角边长分别是3和4，则斜边长是（）

A、3 B、4 C、5 D、6

查看试题解析
3. 一组数据为4，5，7，5，9，则这组数据的众数为（）

A、5 B、4 C、7 D、9

查看试题解析
4. 一次函数 $y = 3 x + 2$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 北京冬奥会U型场地技巧决赛共三轮，甲、乙两位参赛者经过三轮决赛后，他们的平均成绩相同，方差分别是 ${S_{甲}}^{2} = 0.2$ ， ${S_{乙}}^{2} = 0.15$ ．你认为发挥更稳定的是（）

A、甲 B、乙 C、甲和乙一样 D、不能确定

查看试题解析
6. 若点 $A (1 ， a)$ 在一次函数 $y = 2 x - 1$ 图象上，则a的值是（）

A、1 B、3 C、 $- 1$ D、 $\frac{1}{2}$

查看试题解析
7. 下列计算正确的是（）

A、 $2 \sqrt{5} - \sqrt{5} = 1$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{5} \times \sqrt{2} = \sqrt{10}$

查看试题解析
8. 如图，下列条件中，不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B = C D$ ， $B C = A D$ B、 $∠ A = ∠ C$ ， $∠ B = ∠ D$ C、 $A B ∥ C D$ ， $B C = A D$ D、 $A B ∥ C D$ ， $A B = C D$

查看试题解析
9. 下列曲线中不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
10. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）的矩形叫黄金矩形，黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，如希腊的巴特神庙等．若黄金矩形的长为 $\sqrt{5}$ ，则该黄金矩形的宽是（）

A、 $\sqrt{5} - 1$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{5 + \sqrt{5}}{2}$ D、 $\frac{5 - \sqrt{5}}{2}$

查看试题解析

二、填空题

11. 计算： $\sqrt{16}$ = ．

查看试题解析
12. 将函数y＝3x－4 的图像向上平移5个单位长度，所得图像对应的函数表达式为．

查看试题解析
13. 如图，在菱形 $A B C D$ 中， $∠ D = 120 °$ ，则 $∠ 1 =$ 度．

查看试题解析
14. 小丽的笔试成绩为100分，面试成绩为90分，若笔试成绩、面试成绩分别赋权6，4．根据这样的赋权，小丽的平均成绩是分．

查看试题解析
15. 如图，在 $△ A B C$ 中， $D$ ， $E$ ， $F$ 分别是 $A B$ ， $B C$ ， $C A$ 的中点，若 $△ A B C$ 的周长是12，则 $△ D E F$ 的周长是．

查看试题解析
16. 如图，有一架梯子斜靠在与地面 $O M$ 垂直的墙 $O N$ 上，在墙角点 $O$ 处有一只猫紧紧盯住位于梯子 $A B$ 正中间点 $P$ 处的老鼠，等待与老鼠距离最小时扑捉，把梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，若梯子 $A$ 端沿墙下滑，且梯子 $B$ 端沿地面向右滑行．在此滑动过程中，猫与老鼠的距离将（填“变大”、“变小”或“不变”）．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $E$ 是 $A D$ 的中点，将 $△ A B E$ 沿 $B E$ 折叠后得到 $△ G B E$ ，延长 $B G$ 交 $C D$ 于点 $F$ 点，若 $C F = 1$ ， $F D = 2$ ，则 $B C$ 的长为．

查看试题解析

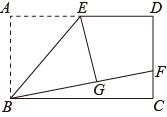
三、解答题

18. 计算： $\sqrt{3} \times \sqrt{2} - \frac{\sqrt{12}}{\sqrt{2}} + | - \sqrt{24} |$ ．

查看试题解析
19. 世界读书日某学校开展了“书香满校园，阅读伴成长”的知识竞赛活动，为了解竞赛情况，随机抽取了10名学生的成绩（竞赛成绩均为整数，满分10分），成绩如下：6，5，8，7，10，7，9，8，4，7．
根据以下信息回答下列问题：

(1)、这10名学生成绩的中位数是；

(2)、在抽取的10名学生中，小明的成绩为8分．你认为小明的成绩如何？请说明理由．

查看试题解析
20. 如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．求证：四边形ABED是平行四边形．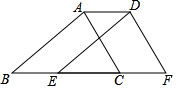

查看试题解析
21. 一个矩形的长为 $a = \sqrt{6} + \sqrt{5}$ ，宽为 $b = \sqrt{6} - \sqrt{5}$ ．

(1)、该矩形的面积＝，周长＝；

(2)、求 $a^{2} + b^{2}$ 的值．

查看试题解析
22. 水是生命之源，节约用水是每个公民应尽的义务．水龙头关闭不严会造成滴水，为了调查水量与漏水时间的关系，某同学在滴水的水龙头下放置了一个能显示水量的容器，每 $5 m i n$ 记录一次容器中的水量如下表：
时间 $t / m i n$
0
5
10
15
20
…
水量 $v / m L$
0
25
50
75
100
…

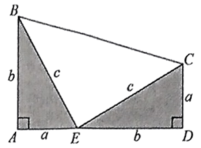
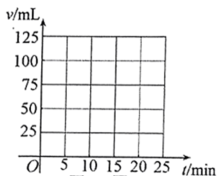(1)、请根据上表中的信息，在图中描出以上述实验所得数据为坐标的各点；

(2)、根据（1）中各点的分布规律，求出v关于t的函数解析式；

(3)、请估算这种漏水状态下一天的漏水量．

查看试题解析
23. 数学之美，不仅是几何图形经过排列组合后呈现的炫美图案，还包括严谨推理引发的思维律动．已超过400种勾股定理的证明方法呈现的数学之美让我们陶醉，其中一种方法是：将两个全等的 $R t △ A B E$ 和 $R t △ D E C$ 如图所示摆放，使点 $A$ ， $E$ ， $D$ 在同一条直线上， $∠ A = ∠ D = 90 °$ 中，即可借助图中几何图形的面积关系来证明 $a^{2} + b^{2} = c^{2}$ ．请写出证明过程．

查看试题解析
24. 如图，在 $▱ A B C D$ 中， $A C$ ， $B D$ 相交于点 $O$ ， $A B = A D$ ， $A C = 8$ ， $B D = 6$ ， $C E ∥ B D$ ， $B E ∥ A C$ ，连接 $O E$ ， $B C$ 与 $O E$ 相交于点 $P$ ，连接 $D P$ ．

(1)、求 $A B$ 的长；

(2)、求证： $O E = A D$ ；

(3)、求 $D P$ 的长．

查看试题解析
25. 如图，在平面直角坐标系中，一次函数 $y = x + b$ 的图象与 $x$ 轴， $y$ 轴分别交于A，B两点，与正比例函数 $y = - 2 x$ 的图象交于点C，点C的纵坐标为4．

(1)、求A，B，C三点的坐标；

(2)、若动点P在射线 $C A$ 上运动，当 $△ O A P$ 的面积是 $△ O B C$ 的面积的 $\frac{1}{8}$ 时，求点P的坐标；

(3)、若点 $Q (m ， 2)$ 在 $△ O B C$ 的内部（不包括边界），请直接写出m的取值范围．

查看试题解析

时间 $t / m i n$	0	5	10	15	20	…
水量 $v / m L$	0	25	50	75	100	…