山西省吕梁市交口县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 已知是整数,则自然数m的所有可能值的个数为( )A、3个 B、4个 C、5个 D、无数个4. 中学篮球队13名队员的年龄情况如下,则这个队队员年龄的众数和中位数为( )
年龄(岁)
14
15
16
17
18
人数(人)
1
4
3
3
2
A、15,16 B、3,4 C、16,15 D、4,35. 如图,某公园的一块草坪旁边有一条直角小路,公园管理处为了方便群众,沿修了一条近路,已知米,米,则走这条近路可以少走( )米路 A、30 B、20 C、50 D、406. 将直线沿y轴向上平移5个单位长度,所得到的直线不经过第( )象限A、一 B、二 C、三 D、四7. 如图,四边形ABCD和AECF都是菱形,点E , F在对角线BD上,∠ABC=60°,∠AEC=120°, ,则AB=( )
A、30 B、20 C、50 D、406. 将直线沿y轴向上平移5个单位长度,所得到的直线不经过第( )象限A、一 B、二 C、三 D、四7. 如图,四边形ABCD和AECF都是菱形,点E , F在对角线BD上,∠ABC=60°,∠AEC=120°, ,则AB=( )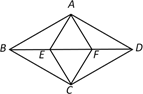 A、 B、 C、 D、8. 如图所示的网格是正方形网格,A,B,C,D是网格线交点,则与的大小关系为( )
A、 B、 C、 D、8. 如图所示的网格是正方形网格,A,B,C,D是网格线交点,则与的大小关系为( )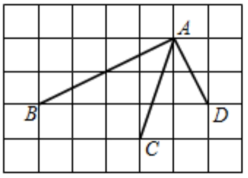 A、 B、 C、 D、无法确定9. 如图,正方形的两条对角线相交于点O,点E在上,且 , 则的度数为( )
A、 B、 C、 D、无法确定9. 如图,正方形的两条对角线相交于点O,点E在上,且 , 则的度数为( ) A、 B、 C、 D、10. 如图(1),点P是边上一动点,沿→→→的路径移动,设点P经过的路径长为x,的面积是y,图(2)是点P运动时y随x变化的关系图象,则与间的距离是( )
A、 B、 C、 D、10. 如图(1),点P是边上一动点,沿→→→的路径移动,设点P经过的路径长为x,的面积是y,图(2)是点P运动时y随x变化的关系图象,则与间的距离是( ) A、5 B、4 C、 D、
A、5 B、4 C、 D、二、填空题
-
11. 若式子成立,则 .12. 有甲,乙两组数据,如表所示,甲,乙两组数据的方差分别为 , , 则(选填“>”,“<”或“=”)
甲
10
12
13
14
16
乙
12
12
13
14
14
13. 如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为 . 14. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(−3,0),则点C到y轴的距离是 .
14. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(−3,0),则点C到y轴的距离是 . 15. 如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,以AB为边作菱形ABCD,轴,则菱形ABCD的周长是 .
15. 如图,在平面直角坐标系中,一次函数的图像与x轴、y轴分别交于点A、B,以AB为边作菱形ABCD,轴,则菱形ABCD的周长是 .
三、解答题
-
16. 计算:(1)、;(2)、 .17. 某校秉承“学会生活,学会学习,学会做人”的办学理念,将本校的办学理念做成宣传牌(AB),放置在教室的黑板上面(如图所示).在三月雷锋活动中小明搬来一架梯子(AE=5米)靠在宣传牌(AB)A处,底端落在地板E处,然后移动的梯子使顶端落在宣传牌(AB)的B处,而底端E向外移到了1米到C处(CE=1米).测量得BM=4米.求宣传牌(AB)的高度(结果用根号表示).
 18. 眠是机体复原整合和巩固记忆的重要环节,对促进中小学生大脑发育、骨骼生长、视力保护、身心健康和提高学习能力与效率至关重要,为了解教育部发布的《关于进一步加强中小学生睡眠管理工作的通知》的实施成效,某调查组随机调查了某学校部分初中生的睡眠时间,根据睡眠时间分成A,B,C,D,E五组,假设平均每天的睡眠时间为x小时,以下是部分数据和不完整的统计图表.
18. 眠是机体复原整合和巩固记忆的重要环节,对促进中小学生大脑发育、骨骼生长、视力保护、身心健康和提高学习能力与效率至关重要,为了解教育部发布的《关于进一步加强中小学生睡眠管理工作的通知》的实施成效,某调查组随机调查了某学校部分初中生的睡眠时间,根据睡眠时间分成A,B,C,D,E五组,假设平均每天的睡眠时间为x小时,以下是部分数据和不完整的统计图表.组别
睡眠时间
频数
A
6≤x<7
2
B
7≤x<8
6
C
8≤x<9
a
D
9≤x<10
18
E
10≤x
4

请结合以上信息回答下列问题:
(1)、直接写出a= , b=;(2)、本次抽查的学生平均每天睡眠时间的中位数落在组;(3)、根据“通知”要求,初中生睡眠时间要达到9小时.该校有1800名学生,根据抽样调查结果,估计该校学生平均每天睡眠时间低于9小时的人数.19. 图,在平行四边形ABCD中,过点D作于点E,点F在边CD上,且 , 连接AF、BF. (1)、求证:四边形DEBF是矩形;(2)、若AF平分 , , , 求BF的长.20. 阅读下列一段文字,回答问题.
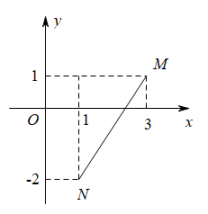
(1)、求证:四边形DEBF是矩形;(2)、若AF平分 , , , 求BF的长.20. 阅读下列一段文字,回答问题.【材料阅读】平面内两点M(),N(),则由勾股定理可得,这两点间的距离MN= . 例如,M(3,1),N(1,-2),则MN=
【直接应用】
(1)、已知P(2,-3),Q(-1,3),求P、Q两点间的距离;(2)、如图,在平面直角坐标系中,A(-1,-3),OB= , OB与x轴正半轴的夹角是45°.
①求点B的坐标;
②试判断△ABO的形状.
21. 为加强学生的劳动教育,某校准备开展以“种下希望,共建美好家园”为主题的义务植树活动. 经了解,购买2棵枣树和3棵石榴树共需44元;购买5棵枣树和6棵石榴树共需98元,该校决定购买棵枣树和50棵石榴树.(1)、求枣树和石榴树的单价;(2)、实际购买时,商家给出了如下优惠方案:方案一:均按原价的九折销售;
方案二:如果购买的枣树不超过50棵,按原价销售. 如果购买的枣树超过50棵,则超出的部分按原价的八折销售,石榴树始终按原价销售.
分别求出两种方案的费用 , 关于的函数解析式.

