山西省临汾市侯马市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 要使分式有意义,则x的取值范围是( )A、x≠3 B、x≠-3 C、x≥3 D、x≥-32. 矩形具有而菱形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分3. 一次函数y=3x-2的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 在▱ABCD中,∠A=3∠B,则∠B的度数是( )A、30° B、36° C、45° D、60°5. 下列说法正确的是( )A、一组数据只有一个众数 B、方差越大,数据越集中 C、一组数据一定只有一个中位数 D、平均数可以用来代表一组数据的离散程度6. 在同一坐标系中,函数 和 的图像大致是( )A、
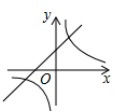 B、
B、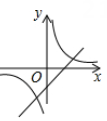 C、
C、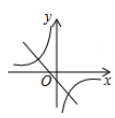 D、
D、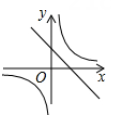 7. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-28. 如图,平行四边形ABCD中,对角线AC、BD相交于O,过点O作OE⊥AC交AD于点E,若AE=4,DE=3,AB=5,则AC的长为( )
7. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-28. 如图,平行四边形ABCD中,对角线AC、BD相交于O,过点O作OE⊥AC交AD于点E,若AE=4,DE=3,AB=5,则AC的长为( )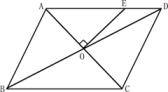 A、 B、 C、 D、9. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )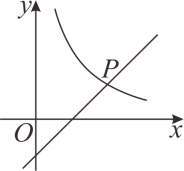 A、 B、 C、 D、10. 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列四个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;其中错误的是( )
A、 B、 C、 D、10. 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列四个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;其中错误的是( )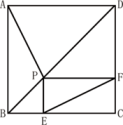 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
11. 人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为.将0.000052用科学记数法表示为.12. 期末数学总成绩是将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末成绩分别是90分,80分,100分,则小红期末数学总成绩是 .13. 在函数y=(k<0)的图象上有三个点(-2,y1),(-1,y2)( , y3),函数值y1、y2、y3的大小用“<”表示是 .14. 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足分别为E、F.求PE+PF= .
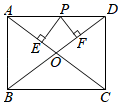 15. 如图,以Rt△ABC斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,连接CO,若AC=4,CO=6,则BC= .
15. 如图,以Rt△ABC斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,连接CO,若AC=4,CO=6,则BC= .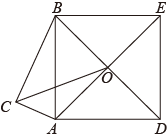
三、解答题
-
16.(1)、计算:(1-π)0×-(-)-1+︱-2︱(2)、先化简,再求值:(-)÷ ,其中x=-3.17. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连接CF,
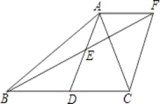 (1)、求证:BD=DC;(2)、如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论.18. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)、求证:BD=DC;(2)、如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论.18. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.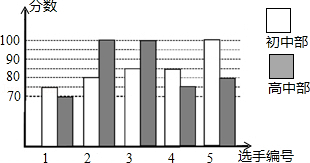 (1)、根据图示填写下表;
(1)、根据图示填写下表;平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)、结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.19. 如图,在矩形ABCD中,E是BC边上的点,AE=BC ,DF⊥AE,垂足为F,连接DE。 (1)、求证:AB=DF;(2)、若CE=1,AF=3,求DF的长。20. 为了支援本地政府抗击“新冠肺炎疫情,某校学生会发起了“献爱心,自愿捐款”活动,已知第一次捐款总额是4800元,第二次捐款总额是5000元,而第二次捐款人数比第一次多了20人,两次人均捐款数恰好相等.求第一次参加捐款的人数.21. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角AC、BD交于点O,AC平分∠BAD.
(1)、求证:AB=DF;(2)、若CE=1,AF=3,求DF的长。20. 为了支援本地政府抗击“新冠肺炎疫情,某校学生会发起了“献爱心,自愿捐款”活动,已知第一次捐款总额是4800元,第二次捐款总额是5000元,而第二次捐款人数比第一次多了20人,两次人均捐款数恰好相等.求第一次参加捐款的人数.21. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角AC、BD交于点O,AC平分∠BAD.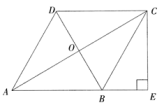 (1)、求证:四边形ABCD是菱形;(2)、过点C作CE⊥AB交AB的延长线于点E,若AB=13,BD=10,求CE的长.22. 如图1,两个完全相同的矩形ABCD,BEGF按如图方式放置,AB=BE,AD=BF,将矩形BEGF绕点B按顺时针旋转,旋转角为 .
(1)、求证:四边形ABCD是菱形;(2)、过点C作CE⊥AB交AB的延长线于点E,若AB=13,BD=10,求CE的长.22. 如图1,两个完全相同的矩形ABCD,BEGF按如图方式放置,AB=BE,AD=BF,将矩形BEGF绕点B按顺时针旋转,旋转角为 .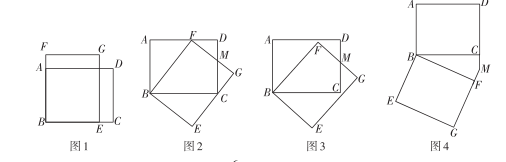 (1)、操作猜想:
(1)、操作猜想:将四边形BEGF绕点B按顺时针方向旋转,当转到如图2所示的位置,点F恰好落在线段AD上,FG与CD交于点M,请直接写出DM和GM的数量关系为:
(2)、继续探究如图3,矩形BEGF绕点B继续按照顺时方向旋转,FG与CD交于点M,试判断(1)中的结论是否仍然成立,若成立请证明;若不成立,请说明理由
(3)、如图4,若 , 在矩形BEFG绕点B继续按顺时针方向旋转的过程中,GF的延长线与DC的延长线交于点M,试判断(1)中的结论是否仍然成立,若成立请证明;若不成立,请说明理由23. 如图,直线y=-x-2分别交x轴、y轴于A、B两点,与双曲线y=(m≠0)在第二象限内的交点为C,CD⊥y轴于点D,且CD=4.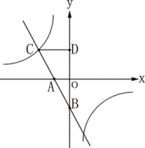 (1)、求双曲线的解析式;(2)、设点Q是双曲线上的一点,且△QOB的面积是△AOB的面积的2倍,求点Q的坐标;(3)、在y轴上存在点P,使PA+PC最短,请直接写出点P的坐标.
(1)、求双曲线的解析式;(2)、设点Q是双曲线上的一点,且△QOB的面积是△AOB的面积的2倍,求点Q的坐标;(3)、在y轴上存在点P,使PA+PC最短,请直接写出点P的坐标.