山东省枣庄市山亭区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 一个不等式的解在数轴上表示如图,则这个不等式可以是( )
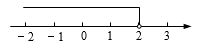 A、 B、 C、 D、2. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )
A、 B、 C、 D、2. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 根据表格中的信息,y可能为( )
3. 根据表格中的信息,y可能为( )x
…
-2
-1
0
1
2
…
y
…
*
无意义
*
-1
*
…
A、 B、 C、 D、4. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )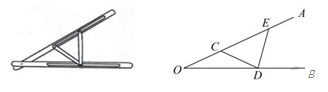 A、60° B、65° C、75° D、80°5. 如图,函数与的图象相交于点 , 则关于x的不等式的解集( )
A、60° B、65° C、75° D、80°5. 如图,函数与的图象相交于点 , 则关于x的不等式的解集( ) A、 B、 C、 D、6. 如图,在 中, , ,尺规作图如下:分别以点 、点 为圆心,大于 为半径作弧,连接两弧交点的直线交 于点 ,连接 ,则 的度数为( )
A、 B、 C、 D、6. 如图,在 中, , ,尺规作图如下:分别以点 、点 为圆心,大于 为半径作弧,连接两弧交点的直线交 于点 ,连接 ,则 的度数为( ) A、 B、 C、 D、7. 相邻边长为a,b的矩形,若它的周长为20,面积为24,则的值为( )A、480 B、240 C、120 D、1008. 小敏利用最近学习的数学知识,给同伴出了这样一道题:假如你从点A出发,沿直线走10米后向左转度,接着沿直线前进10米后,再向左转度……如此下去,当她第一次回到A点时,发现自己走了100米,则的度数为( )
A、 B、 C、 D、7. 相邻边长为a,b的矩形,若它的周长为20,面积为24,则的值为( )A、480 B、240 C、120 D、1008. 小敏利用最近学习的数学知识,给同伴出了这样一道题:假如你从点A出发,沿直线走10米后向左转度,接着沿直线前进10米后,再向左转度……如此下去,当她第一次回到A点时,发现自己走了100米,则的度数为( ) A、36° B、40° C、45° D、60°9. 下列各组多项式中,没有公因式的是( )A、ax﹣bx和by﹣ay B、3x﹣9xy和6y2﹣2y C、x2﹣y2和x﹣y D、a+b和a2﹣2ab+b210. 如图,将△ABC绕顶点A逆时针旋转一定角度得到△ADE,使点B落在DE边上,此时恰好 , 已知∠E=35°,则∠BAE为( )
A、36° B、40° C、45° D、60°9. 下列各组多项式中,没有公因式的是( )A、ax﹣bx和by﹣ay B、3x﹣9xy和6y2﹣2y C、x2﹣y2和x﹣y D、a+b和a2﹣2ab+b210. 如图,将△ABC绕顶点A逆时针旋转一定角度得到△ADE,使点B落在DE边上,此时恰好 , 已知∠E=35°,则∠BAE为( ) A、15° B、20° C、25° D、35°
A、15° B、20° C、25° D、35°二、填空题
-
11. 分解因式: .12. 计算 , 正确的结果是 .13. 如图,P是▱ABCD内部的任意一点,连接AP,DP,BP,CP.若△PAD的面积为 , △PBC的面积为 , 且 , 则▱ABCD的面积是 .
 14. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC;连接DE,F为DE中点,连接BF.若AC=8,BC=6,则BF的长为 .
14. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC;连接DE,F为DE中点,连接BF.若AC=8,BC=6,则BF的长为 . 15. 在平面直角坐标系中,将点M(2,3)向左平移3个单位,再向下平移2个单位,则平移后的点的坐标是 .16. 数学家斐波那契编写的《算经》中有如下问题:一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第一次分钱的人数,设第一次分钱的人数为x人,则可列方程。
15. 在平面直角坐标系中,将点M(2,3)向左平移3个单位,再向下平移2个单位,则平移后的点的坐标是 .16. 数学家斐波那契编写的《算经》中有如下问题:一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第一次分钱的人数,设第一次分钱的人数为x人,则可列方程。三、解答题
-
17. 以下是圆圆解不等式组
的解答过程.
解:由①,得 ,
所以 .
由②,得 ,
所以 ,
所以 .
所以原不等式组的解是 .
圆圆的解答过程是否有错误?如果有错误,写出正确的解答过程.
18.(1)、把下面四个图形拼成一个大长方形,并据此写出一个多项式的因式分解. (2)、已知的三边长为a,b,c,且满足 , 请判断的形状.19. 先化简: ,再从-1,0,1,2中选择一个适合的数代入求值.20. 如图,在△ABC中, , ∠B=60°,∠C=45°.
(2)、已知的三边长为a,b,c,且满足 , 请判断的形状.19. 先化简: ,再从-1,0,1,2中选择一个适合的数代入求值.20. 如图,在△ABC中, , ∠B=60°,∠C=45°. (1)、用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)(2)、若(1)中的角平分线交AC于点D,求△BDC的面积.21. 已知:将▱ABCD纸片折叠,使得点C落在点A的位置,折痕为EF,连接CE.求证:四边形AFCE为平行四边形.
(1)、用尺规作图的方法作出∠B的角平分线;(保留作图痕迹,不写作法)(2)、若(1)中的角平分线交AC于点D,求△BDC的面积.21. 已知:将▱ABCD纸片折叠,使得点C落在点A的位置,折痕为EF,连接CE.求证:四边形AFCE为平行四边形.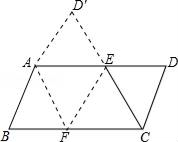 22. 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连接ED,EC.
22. 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连接ED,EC. (1)、试说明△ADC与△BEC全等的理由;(2)、试判断△DCE的形状,并说明理由.23. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段 的端点都在格点上.要求以 为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
(1)、试说明△ADC与△BEC全等的理由;(2)、试判断△DCE的形状,并说明理由.23. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段 的端点都在格点上.要求以 为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.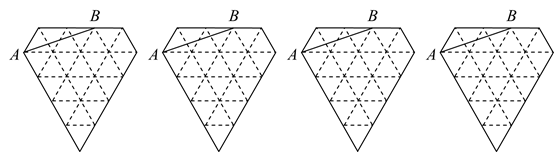 24. 某学校在疫情防控工作中,计划同时购买一定数量的75%酒精消毒液和84消毒液.已知75%酒精消毒液比84消毒液单价每桶高6元,用1200元购进的75%酒精消毒液和960元购进的84消毒液数量相同;(1)、75%酒精消毒液和84消毒液每桶单价分别是多少元?(2)、该校计划购进75%酒精消毒液和84消毒液共100桶,可用于购买这两种商品的资金不超过2680元.试问:75%酒精消毒液最多买多少桶?
24. 某学校在疫情防控工作中,计划同时购买一定数量的75%酒精消毒液和84消毒液.已知75%酒精消毒液比84消毒液单价每桶高6元,用1200元购进的75%酒精消毒液和960元购进的84消毒液数量相同;(1)、75%酒精消毒液和84消毒液每桶单价分别是多少元?(2)、该校计划购进75%酒精消毒液和84消毒液共100桶,可用于购买这两种商品的资金不超过2680元.试问:75%酒精消毒液最多买多少桶?