山东省烟台市龙口市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{3 \frac{1}{3}}$ B、 $\sqrt{33}$ C、 $\sqrt{\frac{1}{27}}$ D、 $\sqrt{0.3}$

查看试题解析
2. 以下四组线段，成比例的是（）

A、 $2 c m ， 3 c m ， 4 c m ， 6 c m$ B、 $2 c m ， 4 c m ， 6 c m ， 8 c m$ C、 $3 c m ， 4 c m ， 5 c m ， 6 c m$ D、 $4 c m ， 6 c m ， 6 c m ， 8 c m$

查看试题解析
3. 已知 $\frac{x}{y} = \frac{3}{5}$ ，则 $\frac{x}{x + y}$ 的值为（）

A、 $\frac{2}{5}$ B、 $\frac{3}{8}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 关于x的一元二次方程ax²﹣2x+1＝0有两个不相等的实数根，则a的取值范围是（）

A、a≤1 B、a＜1 C、a≤1且a≠0 D、a＜1且a≠0

查看试题解析
5. 下列四个表格表示的变量关系中，变量y是x的反比例函数的是（）

A、
－x
…
－2
－1
－1
－2
…
－y
…
－6
－4
0
－2
…
B、
x
…
－2
－1
1
2
…
y
…
－6
－3
3
6
…
C、
x
…
－2
－1
1
2
…
y
…
3
6
－6
－3
…
D、
x
…
－2
－1
1
2
…
y
…
2
1
－1
－2
…

查看试题解析
6. 如图，已知∠A=70°，∠APC=65°， $A C^{2} = A P \cdot A B$ ，则∠B的度数为（）

A、45° B、50° C、55° D、60°

查看试题解析
7. 由下表估算一元二次方程 $x^{2} + 12 x - 15 = 0$ 的一个根的范围，正确的是（）
$x$
1.0
1.1
1.2
1.3
$x^{2} + 12 x$
13
14.41
15.84
17.29

A、 $1.0 < x < 1.1$ B、 $1.1 < x < 1.2$ C、 $1.2 < x < 1.3$ D、 $14.41 < x < 15.84$

查看试题解析
8. 某商品原价200元，连续两次降价后，售价为108元，若设每次降价的百分率都是x，则下列所列方程正确的是（）

A、200（1+x）²=108 B、200（1+x）=108 C、200（1-x）=108 D、200（1-x）²=108

查看试题解析
9. 若点A（﹣4，y₁）、B（﹣2，y₂）、C（2，y₃）都在反比例函数 $y = - \frac{1}{x}$ 的图象上，则y₁、y₂、y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₃＞y₂＞y₁ C、y₂＞y₁＞y₃ D、y₁＞y₃＞y₂

查看试题解析
10. 已知a满足 $| 2021 - a | + \sqrt{a - 2022} = a$ ，则 $a - 202 1^{2}$ 的值为（）

A、0 B、1 C、2021 D、2022

查看试题解析

二、填空题

11. 若式子 $\frac{1}{\sqrt{2 - 3 x}}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 如图，已知D、E分别为AB、AC上的两点，且DE $∥$ BC，AE=3CE，AB=8，则AD的长为．

查看试题解析
13. 如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，OP=AB，四边形ABPO的面积为6，则这个反比例函数的表达式为．

查看试题解析
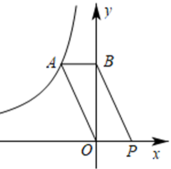14. 小颖在地面E处放一面镜子，当他垂直于地面AC站立于点C处时，刚好能从镜子中看到教学楼的顶端B，FE⊥AC，根据光的反射定律有∠FEB=∠FED，此时EA=20米，CE=2.5米．已知眼睛距离地面的高度DC=1.6米，则教学楼的高度为米．

查看试题解析
15. 已知 $x = \frac{- 3 + \sqrt{5}}{2}$ ，那么 $2 x^{2} + 6 x - 3$ 的值是．

查看试题解析
16. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF= $\sqrt{2}$ AF；③DF=DC；④ $\frac{{S_{△}}_{A B F}}{S_{四边形 C D E F}} = \frac{2}{5}$ ，其中正确结论的序号为．

查看试题解析

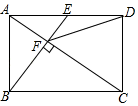
三、解答题

17. 计算：

(1)、 $\sqrt{18} \div （ 3 \sqrt{2} + \sqrt{8} ）$ ；

(2)、 $(\sqrt{6} - \sqrt{\frac{1}{2}}) \times 3 \sqrt{\frac{2}{3}}$ ；

查看试题解析
18. 已知a＝2＋ $\sqrt{3}$ ， b＝2－ $\sqrt{3}$ ．求a²b＋ab²的值．

查看试题解析
19. 解方程：

(1)、3x²-5x+1=0（配方法）；

(2)、(x+3)(x-1)=5（公式法）．

查看试题解析
20. 如图，△ABC的三个顶点的坐标分别为A（3，1），B（1，2），C（4，3）．以原点O为位似中心，在第一象限内将△ABC放大为原来的2倍得到△A₁B₁C₁ ，作出△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标；

查看试题解析
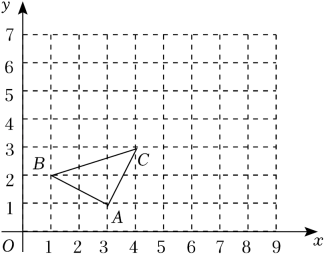21. 如图，已知正比例函数的图象与反比例函数的图象在第二、四象限分别交于A（m，1），B（2n，-n）两点．

(1)、求A，B两点坐标；

(2)、根据图象，当正比例函数值大于反比例函数值时，直接写出x的取值范围．

查看试题解析
22. 某中学兴趣小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边是由周长为30米的篱笆围成.如图所示，已知墙长为20米，设这个苗圃园垂直于墙的一边长为x米

(1)、若苗圃园的面积为108m² ，求x的值，

(2)、苗圃园的面积能达到120m²吗？若能，求出x；若不能，说明理由.

查看试题解析
23. 已知关于x的一元二次方程mx²+4x+4﹣m＝0．

(1)、求证：方程总有两个实数根；

(2)、若m为整数，当此方程有两个互不相等的负整数根时，求m的值；

查看试题解析
24. 如图，直线y=ax+1与x轴、y轴分别相交于A、B两点，与双曲线y= $\frac{k}{x}$ （x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（-2，0）．

(1)、求直线AP和双曲线的表达式；

(2)、若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．

查看试题解析
25. 如图1，△ABC和△ADE均为等腰直角三角形，∠ACB=∠AED=90°，直线BD和直线CE交于点F．

(1)、线段BD与CE具有怎样的数量关系？写出证明过程；

(2)、若AC=BC=3，AE＝DE= $\sqrt{2}$ ，将△ADE绕着点A在平面内旋转，当点D落在线段AC上时，在图2中补全图形，并求CF的长度．

查看试题解析

－x	…	－2	－1	－1	－2	…
－y	…	－6	－4	0	－2	…

x	…	－2	－1	1	2	…
y	…	－6	－3	3	6	…

x	…	－2	－1	1	2	…
y	…	3	6	－6	－3	…

x	…	－2	－1	1	2	…
y	…	2	1	－1	－2	…