山东省威海市乳山市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算中，正确的是（）

A、 $5 \sqrt{7} - 2 \sqrt{7} = 21$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{3} \times \sqrt{6} = 3 \sqrt{2}$ D、 $\sqrt{15} \div \sqrt{5} = 3$

查看试题解析
2. 若 $\frac{a}{b} = 2$ ，则 $\frac{a + b}{a - b}$ =（）

A、3 B、-3 C、 $\frac{3}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 已知关于x的一元二次方程 $2 x^{2} - 8 x + m = 0$ 有一个根是x₁=3，则另一个根x₂是（　　）

A、﹣5 B、﹣3 C、1 D、2

查看试题解析
4. 如果菱形的边长是a，较长对角线为 $\sqrt{3} a$ ，那么菱形的较小内角是（）

A、30° B、45° C、60° D、75°

查看试题解析
5. 已知方程 $x^{2} = m$ 的解是有理数，那么对于下列实数m不能取的数是（）

A、1 B、4 C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
6. 如图，AB//CD，AD与BC交于点O，若AO=2，DO=4，BO=3，则CD的长度不可能为（）

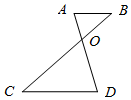A、5 B、7 C、9 D、11

查看试题解析
7. 若a，b，c是△ABC的三边，则关于x的方程 $(a + b) x^{2} - 2 c x + a + b = 0$ 的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
8. 在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把△ABO缩小，则点A的对应点A′的坐标是（　　）

A、（﹣2，1） B、（﹣8，4） C、（﹣8，4）或（8，﹣4） D、（﹣2，1）或（2，﹣1）

查看试题解析
9. 若关于x的一元二次方程 $k^{2} x^{2} + (2 k - 1) x + 1 = 0$ 的两个实数根互为倒数，则k=（）

A、1 B、-1 C、 $± 1$ D、 $- 1 - \sqrt{2}$

查看试题解析
10. 如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，Q为对角线AC上的动点，则△BEQ周长的最小值为（）

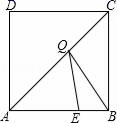A、5 B、6 C、 $4 \sqrt{2}$ D、8

查看试题解析

二、多选题

11. 如图，将 $△$ ABC沿射线BC向右平移到 $△$ DCE，连接AD，BD．添加下列条件，能判断四边形ABCD是菱形的有（）

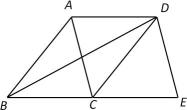A、AC=BD B、AB=AD C、AC⊥BD D、 $△$ ABC为等边三角形

查看试题解析
12. 如图，在四边形ABCD中，∠B=∠C，AB=3，CD=2，BC=6，点P是边BC上的动点，若△ABP与△CDP相似，则BP=（）

A、3.6 B、 $3 - \sqrt{3}$ C、 $3 + \sqrt{3}$ D、2.4

查看试题解析

三、填空题

13. 计算： $\sqrt{27} + \sqrt{\frac{1}{3}} - {(\sqrt{4} - 3)}^{0}$ = ．

查看试题解析
14. 某商场将进价为30元的台灯以单价40元售出，平均每月能售出600个．调查表明：这种台灯的单价每上涨1元，其销售量将减少10个．为实现平均每月10000元的销售利润，从消费者的角度考虑，商场对这种台灯的售价应定为元．

查看试题解析
15. 如图，在直角三角形纸片ABC中，∠ACB=90°，AC=10cm．先沿BC边裁剪一个宽为4cm的矩形纸片，再沿AC边裁剪一个边长为4cm的正方形纸片，点D，E均在AB边上，则BC=cm．

查看试题解析
16. 若 $x_{1} ， x_{2}$ 是方程 $x^{2} - 3 x - 1 = 0$ 的两个实数根，则 ${x_{1}}^{2} - x_{1} + 2 x_{2}$ = ．

查看试题解析
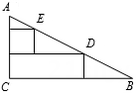17. 如图，AB=BC=CD，AB⊥BC，∠BCD=30°，则∠BAD=°．

查看试题解析
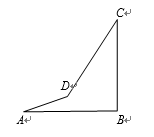18. 如图，在平面直角坐标系中，菱形ABCD的顶点A，C 的坐标分别为（3，3），（-1，-1），对角线BD交AC于点M，交x轴于点N．若BN=2ND，则点D的坐标为．

查看试题解析

四、解答题

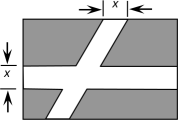
19. 解方程： $2 x^{2} + 3 x = 2$ ．（因式分解法）

查看试题解析
20. 在一块长16m、宽12m的矩形草坪上，要修建如图所示的两条宽均为xm的甬路，并使甬路所占面积为原来矩形草坪面积的一半，求甬路的宽．

查看试题解析
21. 如图，点E是正方形ABCD内一点，连接AE，BE，DE，∠AEB=90°， $S_{Δ A D E} = 4$ ．求AE的长．

查看试题解析
22. 我们曾学习过用尺规法确定线段的中点．具体画法如图Ⅰ：
分析如图的画图痕迹，连接PA，PB，QA，QB，可得PA=PB=QA=QB．依据“全等三角形”“线段垂直平分线”“菱形”等知识，可用不同的方法证明出“点C为线段AB的中点”．

【提出问题】

小明同学经过思考，得出另外一种确定线段中点的画法．

画图方法如图Ⅱ：

①以点A为圆心，AB为半径画出大于半圆的弧，交BA的延长线于点C；

②分别以点B，C为圆心，BA，CB为半径画弧，两弧交于点E；

③以点E为圆心，AB为半径画弧，交线段AB于点F．

画图完成后，小明得出结论：点F为线段AB的中点．

【推理分析】

依据上述画法，请你判断小明同学所得出的结论是否正确．若正确，进行证明；若不正确，说明理由．

查看试题解析
23. 如图，在▱ABCD中，对角线AC，BD交于点O，点E，F是AC上的动点，且不与O点重合．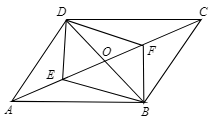

(1)、若AE=CF，求证：四边形DEBF是平行四边形；

(2)、已知BD=12cm，AC=16cm，点E，F均以2cm/s的速度，分别从点A，C出发，向点C，A方向运动．若以D，E，B，F为顶点的四边形是矩形，求点E，F运动时间t的值．

查看试题解析
24. 【材料阅读】
把分母中的根号化去，将分母转化为有理数的过程，叫做分母有理化．
例如：化简 $\frac{1}{\sqrt{2} + 1}$ ．
解： $\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ．
上述化简的过程，就是进行分母有理化．

(1)、化简 $\frac{1}{2 - \sqrt{3}}$ 的结果为：；

(2)、猜想：若n是正整数，则 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 进行分母有理化的结果为：；

(3)、若有理数a，b满足 $\frac{a}{\sqrt{2} - 1} + \frac{b}{\sqrt{2} + 1} = 2 \sqrt{2} - 1$ ，求a，b的值．

查看试题解析
25. 【揭示关系】
如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，则AB=2，AC= $\sqrt{3}$ ．
即 $B C ： A C ： A B = 1 ： \sqrt{3} ： 2$ ．
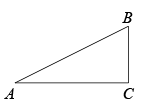
对于上述三角形的三边关系，可以作为问题解决的条件直接使用．
【问题解决】
如图Ⅰ，在Rt△AOB中，∠AOB=90°，∠OAB=30°，点C在边OB上，点D在AO边上，∠OCD=30°．将△OCD绕点O逆时针旋转α（90°<α<180°）后，得到 $△ O C^{'} D^{'}$ ，点C，D的对应点分别为点 $C^{'}$ ， $D^{'}$ ，连接 $A C^{'}$ ， $B D^{'}$ ，得到Ⅱ．

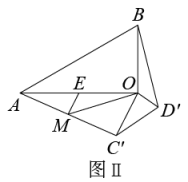(1)、若 $C^{'} D^{'} ∥ A B$ ，求α；

(2)、若点E，M分别是OA， $A C^{'}$ 的中点，连接EM，OM．
①求证： $△ E O M ∽ △ O B D^{'}$ ；
②线段OM和 $B D^{'}$ 之间存在怎样的数量关系和位置关系？写出你的结论，并进行证明．

查看试题解析