山东省临沂市河东区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 下列式子表示y是x的函数的是( )A、x+3y=1 B、 C、|y|=x D、y2=x2. 如果某函数的图象如图所示,那么y随x的增大而( )
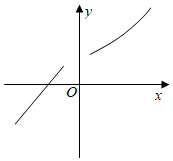 A、增大 B、减小 C、不变 D、有时增大有时减小3. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A、增大 B、减小 C、不变 D、有时增大有时减小3. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )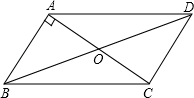 A、18 B、19 C、20 D、214. 如图,从一个大正方形中裁去面积为和的两个小正方形,则剩余部分(阴影部分)的面积等于( )
A、18 B、19 C、20 D、214. 如图,从一个大正方形中裁去面积为和的两个小正方形,则剩余部分(阴影部分)的面积等于( )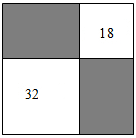 A、 B、 C、 D、5. 在对一组样本数据进行分析时,小华列出了方差的计算公式: , 由公式提供的信息,则下列说法错误的是( )A、样本的众数是3 B、样本的平均数是3 C、样本的总数n=2 D、样本的中位数是36. 如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,修路的方法有 ( )
A、 B、 C、 D、5. 在对一组样本数据进行分析时,小华列出了方差的计算公式: , 由公式提供的信息,则下列说法错误的是( )A、样本的众数是3 B、样本的平均数是3 C、样本的总数n=2 D、样本的中位数是36. 如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,修路的方法有 ( ) A、1种 B、2种 C、4种 D、无数种7. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )
A、1种 B、2种 C、4种 D、无数种7. 匀速地向一个容器注水,最后把容器注满.在注水的过程中,水面高度 随时间 的变化规律如图所示(图中 为一折线),那么这个容器的形状可能是下列图中的( )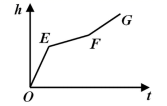 A、
A、 B、
B、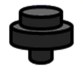 C、
C、 D、
D、 8. 如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕所成锐角的大小为( )
8. 如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕所成锐角的大小为( )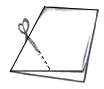 A、30° B、45° C、60° D、90°9. 若成立,则a,b满足的条件是( )A、a<0且b>0 B、a≤0且b≥0 C、a<0且b≥0 D、a,b异号10. 已知一次函数y =(2m+1)x+m-3的图像不经过第二象限,则m的取值范围( )A、m>- B、m<3 C、- <m<3 D、- <m≤311. 若不等式的解集是 , 则下列各点可能在一次函数图象上的是( )A、 B、 C、 D、12. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠BAD=40°,则∠OED的度数为( )
A、30° B、45° C、60° D、90°9. 若成立,则a,b满足的条件是( )A、a<0且b>0 B、a≤0且b≥0 C、a<0且b≥0 D、a,b异号10. 已知一次函数y =(2m+1)x+m-3的图像不经过第二象限,则m的取值范围( )A、m>- B、m<3 C、- <m<3 D、- <m≤311. 若不等式的解集是 , 则下列各点可能在一次函数图象上的是( )A、 B、 C、 D、12. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠BAD=40°,则∠OED的度数为( )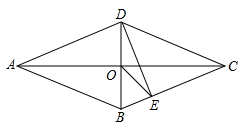 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30°二、填空题
-
13. 若式子 在实数范围内有意义,则x的取值范围是.14. 如图,A,B两地被池塘隔开,小明通过下面的方法测出A,B间的距离:先在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=15米,由此他知道了A,B间的距离为米.
 15. 如图,圆柱的高为6cm,底面周长为16cm,蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程是cm.
15. 如图,圆柱的高为6cm,底面周长为16cm,蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程是cm.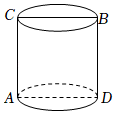 16. 如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为1,L2、L3的距离为2,则正方形的边长为 .
16. 如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为1,L2、L3的距离为2,则正方形的边长为 .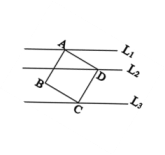
三、解答题
-
17. 已知 , , y>0,求y的值.18. 临沂果农张先生几年前承包了甲、乙两块林地,各栽种200棵桃树,成活率为99%,现已挂果.为分析收成情况,他分别从两块桃园随机抽取5棵树作为样本,并采摘完样本树上的桃子,每棵树的产量如图所示.
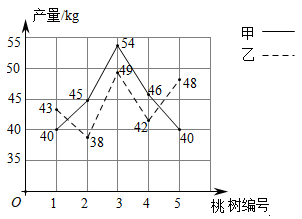 (1)、分别计算甲,乙两块桃园样本的平均数;(2)、请根据样本估算甲,乙两块桃园桃子的总产量;(3)、根据样本,通过计算估计哪块桃园的桃子产量比较稳定.19. 已知函数(1)、画出函数图象;
(1)、分别计算甲,乙两块桃园样本的平均数;(2)、请根据样本估算甲,乙两块桃园桃子的总产量;(3)、根据样本,通过计算估计哪块桃园的桃子产量比较稳定.19. 已知函数(1)、画出函数图象;列表:
x
…
…
y
…
…
描点,连线得到函数图象:
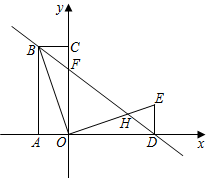
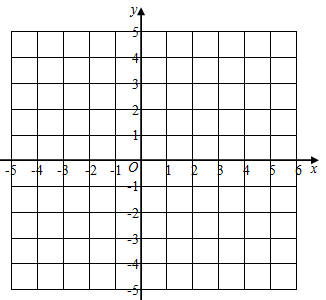 (2)、设(x1 , y1),(x2 , y2)是函数图象上的点,若x1+x2=0,证明:y1+y2=0.20. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,连接DB.
(2)、设(x1 , y1),(x2 , y2)是函数图象上的点,若x1+x2=0,证明:y1+y2=0.20. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,连接DB.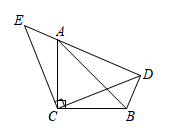 (1)、证明:△ECA≌△DCB(2)、若 , , 求AC的长.
(1)、证明:△ECA≌△DCB(2)、若 , , 求AC的长.