山东省济南市市中区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 已知a>b,则下列各式中错误的是( )A、a-1<b-1 B、-a<-b C、2a>2b D、>2. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、矩形 D、直角三角形3. 将中的a、b都扩大3倍,则分式的值( )A、扩大3倍 B、扩大6倍 C、扩大9倍 D、不变4. 如图,在平行四边形ABCD中,∠A=130°,CE平分∠BCD,则∠AEC的度数是( )
 A、115° B、110° C、105° D、120°5. 关于x的一元二次方程x2+x-a=0的一个根是2,则另一个根是( )A、-1 B、-2 C、-3 D、26. 下列多项式能用完全平方公式分解因式的是( )A、x2-2x-1 B、a2-b2 C、x2-2xy D、a2-6a+97. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、邻边相等的矩形是正方形 C、对角线相等的平行四边形是正方形 D、有一个内角是直角的四边形是矩形8. 关于x的分式方程+=3有增根,则实数m的值是( )A、2 B、-1 C、3 D、49. 某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,该公司11、12两个月营业额的月均增长率,设该公司11、12两个月营业额的月均增长率为x,则根据题意可列的方程为( )A、2500(1+x)2=9100 B、2500[1+(1+x)+(1+x)2]=9100 C、2500[(1+x)+(1+x)2]=9100 D、9100(1+x)2=250010. 如图,菱形ABCD的对角线AC、BD相交于点O,BEAC,AEBD,OE与AB交于点F.若OE=5,AC=8,求菱形ABCD的面积为( )
A、115° B、110° C、105° D、120°5. 关于x的一元二次方程x2+x-a=0的一个根是2,则另一个根是( )A、-1 B、-2 C、-3 D、26. 下列多项式能用完全平方公式分解因式的是( )A、x2-2x-1 B、a2-b2 C、x2-2xy D、a2-6a+97. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、邻边相等的矩形是正方形 C、对角线相等的平行四边形是正方形 D、有一个内角是直角的四边形是矩形8. 关于x的分式方程+=3有增根,则实数m的值是( )A、2 B、-1 C、3 D、49. 某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,该公司11、12两个月营业额的月均增长率,设该公司11、12两个月营业额的月均增长率为x,则根据题意可列的方程为( )A、2500(1+x)2=9100 B、2500[1+(1+x)+(1+x)2]=9100 C、2500[(1+x)+(1+x)2]=9100 D、9100(1+x)2=250010. 如图,菱形ABCD的对角线AC、BD相交于点O,BEAC,AEBD,OE与AB交于点F.若OE=5,AC=8,求菱形ABCD的面积为( ) A、20 B、22 C、24 D、4011. 对于一元二次方程,我国及其他一些国家的古代数学家还研究过其几何解法呢!以方程x2+2x﹣35=0即x(x+2)=35为例加以说明,三国时期的数学家赵爽在其所著的《勾股圆图注》中记载的方法是:构造如图,一方面,图中的大方形的面积是(x+x+2)2;另一方面,它又等于四个矩形面积加上中间小正方形的面积,即4×35+22,据此易得x=5,那么在下面的四个构图中,能够说明x2﹣2x﹣8=0的正确构图是( )
A、20 B、22 C、24 D、4011. 对于一元二次方程,我国及其他一些国家的古代数学家还研究过其几何解法呢!以方程x2+2x﹣35=0即x(x+2)=35为例加以说明,三国时期的数学家赵爽在其所著的《勾股圆图注》中记载的方法是:构造如图,一方面,图中的大方形的面积是(x+x+2)2;另一方面,它又等于四个矩形面积加上中间小正方形的面积,即4×35+22,据此易得x=5,那么在下面的四个构图中,能够说明x2﹣2x﹣8=0的正确构图是( )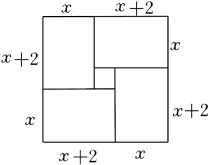 A、
A、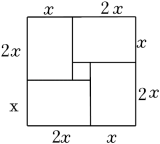 B、
B、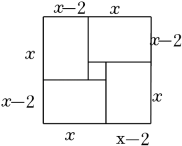 C、
C、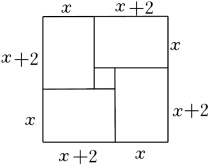 D、
D、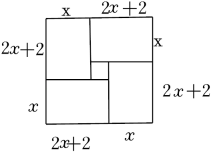 12. 在平面直角坐标系中,对于两个点P、Q和图形W,如果在图形W上存在点M、N(M、N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.已知正方形的边长为2,一边平行于x轴,对角线的交点为点O,点D的坐标为(2,0).若点E(x,2)与点D是正方形的一对平衡点,则x的取值范围为( )
12. 在平面直角坐标系中,对于两个点P、Q和图形W,如果在图形W上存在点M、N(M、N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.已知正方形的边长为2,一边平行于x轴,对角线的交点为点O,点D的坐标为(2,0).若点E(x,2)与点D是正方形的一对平衡点,则x的取值范围为( ) A、-3≤x≤3 B、-4≤x≤4 C、-2≤x≤2 D、-5≤x≤5
A、-3≤x≤3 B、-4≤x≤4 C、-2≤x≤2 D、-5≤x≤5二、填空题
-
13. 分解因式:2a2﹣ab=.14. 如果一个多边形的内角和等于其外角和的两倍,则这个多边形是边形.15.
如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD= .
 16. 如图,直线y=x+1与直线y=ax+b相交于点A(m,3),则关于x的不等式x+1<ax+b的解集是 .
16. 如图,直线y=x+1与直线y=ax+b相交于点A(m,3),则关于x的不等式x+1<ax+b的解集是 . 17. 若关于x的一元二次方程有实数根,则k的取值范围是 .18. 如图,在▱ABCD中,AB=5,AD=3,∠A=60°,E是边AD上且AE=2DE,F是射线AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG,连接BG、DG,则BG-DG的最大值为 .
17. 若关于x的一元二次方程有实数根,则k的取值范围是 .18. 如图,在▱ABCD中,AB=5,AD=3,∠A=60°,E是边AD上且AE=2DE,F是射线AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG,连接BG、DG,则BG-DG的最大值为 .
三、解答题
-
19. 计算:(1)、分解因式:3a3-6a2+3a;(2)、先化简,再求值:其中a=5.20. 解方程:(1)、;(2)、x2-4x+3=0.21. 如图,在ABCD中,点M、N分别是AD、BC上的两点,点E、F在对角线BD上,且DM=BN时,DF=BE,求证:四边形MENF是平行四边形.
 22. 解不等式组: , 并求出它的所有整数解的和.23. 在矩形ABCD中,AB=2cm,BC=8cm,点P从点D出发向点A运动到点A即停止;同时点Q从点B出发向点C运动到点C即停止,点P、Q的速度都是1cm/s,连结PQ、AQ、CP,设点P、Q运动的时间为ts.
22. 解不等式组: , 并求出它的所有整数解的和.23. 在矩形ABCD中,AB=2cm,BC=8cm,点P从点D出发向点A运动到点A即停止;同时点Q从点B出发向点C运动到点C即停止,点P、Q的速度都是1cm/s,连结PQ、AQ、CP,设点P、Q运动的时间为ts. (1)、当t为何值时,四边形ABQP是矩形,请说明理由;(2)、当t为何值时,四边形AQCP是菱形,请说明理由.24. 69中学计划购买A、B两种学习用品奖励学生,已知购买一个A比购买一个B多用20元,若用400元购买A的数量是用160元购买B数量的一半,(1)、求A、B两种学习用品每件多少钱?(2)、经商谈,商店给该校购买一个A奖品赠送一个B奖品的优惠,如果该校需要B奖品的个数是A奖品个数的2倍还多8个,且该学校购买A、B两种奖品的总费用不超过670元,那么该校最多可购买多少个A奖品?25. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法等等.
(1)、当t为何值时,四边形ABQP是矩形,请说明理由;(2)、当t为何值时,四边形AQCP是菱形,请说明理由.24. 69中学计划购买A、B两种学习用品奖励学生,已知购买一个A比购买一个B多用20元,若用400元购买A的数量是用160元购买B数量的一半,(1)、求A、B两种学习用品每件多少钱?(2)、经商谈,商店给该校购买一个A奖品赠送一个B奖品的优惠,如果该校需要B奖品的个数是A奖品个数的2倍还多8个,且该学校购买A、B两种奖品的总费用不超过670元,那么该校最多可购买多少个A奖品?25. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法等等.①分组分解法:
例如:x2-2xy+y2-4=(x2-2xy+y2)-4=(x-y) 2-22=(x-y-2)(x-y+2).
②拆项法:
例如:x2+2x-3=x2+2x+1-4=(x+1) 2-2=(x+1-2) (x+1+2) = (x-1) (x+3).
(1)、分解因式:①4x2+4x-y2+1;
②x2-6x+8;
(2)、已知:a、b、c为△ABC的三条边,a2+b2+c2-4a-4b-6c+17=0,求△ABC的周长.26. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
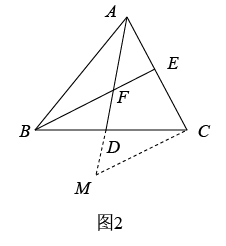

 (1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.
(1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.小明发现可以类比以上思路进行证明.
证明:如图2,延长AD至点M,使MD=FD,连接MC,……
请你根据小明的思路完成证明过程.
(2)、【方法运用】如图3,在菱形ABCD中,∠D=60°,点E为射线BC上一个动点(在点C右侧),把线段EC绕点E逆时针旋转120°得到线段BC′,连接BC′,点F是BC′的中点,连接AE、CF、EF.①请你判断线段EF和AE的数量关系是 ▲ , 并说明理由;
②若菱形ABCD的边长为6,CF=CE,请直接写出CF的长.
27. 矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB,将△ABC沿AB折叠得△ABE,AE交y轴于点D,线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD. (1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD,当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q,使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
(1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD,当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q,使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.