江西省萍乡市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. $4 m^{2} n^{2}$ 与 $6 m n^{2}$ 的公因式是（）

A、 $m^{2} n^{2}$ B、4mm C、2mm D、 $12 m^{2} n^{2}$

查看试题解析
2. 下列定理中没有逆定理的是（）

A、内错角相等，两直线平行 B、直角三角形中，两锐角互余 C、等腰三角形两底角相等 D、对顶角相等

查看试题解析
3. 不等式 $\frac{4 - x}{3} > x$ 的解集是（）

A、 $x < 1$ B、 $x < - 1$ C、 $x > 1$ D、 $x > - 1$

查看试题解析
4. 如图的网格中，点A、B在格点上，在网格上找到点C，使 $△ A B C$ 为等腰三角形，这样的点C共有（）

A、8个 B、9个 C、10个 D、11个

查看试题解析
5. 解关于x的方程 $\frac{x - 6}{x - 2} = \frac{a}{x - 2}$ 产生增根，则常数a的值等于（）

A、-5 B、-4 C、-3 D、2

查看试题解析
6. 如图，六边形 $A B C D E F$ 的每个内角相等，若 $∠ 1 = 58 °$ ，则 $∠ 2$ 的度数为（）

A、58° B、59° C、60° D、61°

查看试题解析
7. 已知关于x不等式组 ${\begin{array}{l} 2 x - 3 a < 2 \\ x - 2 b > 3 \end{array}$ 的解集为 $- 1 < x < 2$ ，则代数式 $(a - \frac{b^{2}}{a}) \cdot \frac{a}{a - b}$ 的值是（）

A、 $\frac{2}{3}$ B、-2 C、 $- \frac{8}{3}$ D、 $- \frac{4}{3}$

查看试题解析
8.
如图，在边长为 $\sqrt{3}$ 的等边三角形ABC中，过点C垂直于BC的直线交∠ABC的平分线于点P，则点P到边AB所在直线的距离为（　　）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3}$ D、1

查看试题解析
9. 甲志愿者计划用若干个工作日完成社区的某项工作，从第三个工作日起，乙志愿者加盟此项工作，且甲、乙两人工效相同，结果提前3天完成任务，则甲志愿者计划完成此项工作的天数是（）

A、8 B、7 C、6 D、5

查看试题解析
10. 如图， $△ A B C$ 的周长为21，点D、E在边 $B C$ 上， $∠ A B C$ 的平分线垂直于 $A E$ ，垂足为N， $∠ A C B$ 的平分线垂直于 $A D$ ，垂足为M，若 $B C = 9$ ，则 $M N$ 的长度为（）

A、1.5 B、2 C、2.5 D、3

查看试题解析

二、填空题

11. 分解因式 $m^{3} - 4 m^{2} + 4 m =$ ．

查看试题解析
12. 如图，在 $△ A B C$ 中， $D E$ 是 $A C$ 的垂直平分线，分别交 $B C$ ， $A C$ 于D，E， $A E = 4 c m$ ， $△ A B D$ 的周长为14cm，则 $△ A B C$ 的周长为cm．

查看试题解析
13. 如图是一个正方形，分成四部分，其面积分别为 $a^{2}$ ， $a b$ ， $a b$ ， $b^{2}$ ，则原正方形的边长是．

查看试题解析
14. 如图，△ABC是等边三角形，AD是BC边上的高，E是AC上一点，且AE＝AD，则∠AED的度数为。

查看试题解析
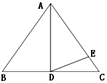15. 甲、乙两个工程队合修一条公路，已知甲工程队每天修 $(a^{2} - 4)$ 米，乙工程队每天修 ${(a - 2)}^{2}$ 米（其中 $a > 2$ ），则甲工程队修900米所用时间与乙工程队修600米所用时间的比值是．（用含a的式子表示）

查看试题解析
16. 设实数a，b满足 $\frac{a}{b} + \frac{b}{a} = 2$ ，则分式 $\frac{a^{2} + a b + b^{2}}{a^{2} + 4 a b + b^{2}}$ 的值是．

查看试题解析
17. 如图，E、F分别是平行四边形 $A B C D$ 的边 $A B$ 、 $C D$ 上的点， $A F$ 与 $D E$ 相交于点P， $B F$ 与 $C E$ 相交于点 $Q$ ，若S_△APD=15cm² ， $S_{△ B Q C} = 25 c m^{2}$ ，则阴影部分的面积为 $c m^{2}$ ．

查看试题解析
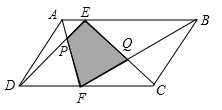18.
如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．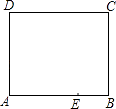

查看试题解析

三、解答题

19.

(1)、先化简： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后从0，1，2三个数中选择一个恰当的数代人求值．

(2)、解方程： $\frac{x}{x^{2} - 4} + \frac{2}{x + 2} = \frac{1}{x - 2}$

查看试题解析
20. 解不等 ${\begin{matrix} 3 x - 5 < x + 1 \\ \frac{3 x - 4}{6} ⩽ \frac{2 x - 1}{3} \end{matrix}$ 式组，并把解集在数轴上表示出来.

查看试题解析
21. 如图，在平面直角坐标系中，每个小方格都是边长为1的正方形， $△ A B C$ 的顶点均在格点上，点A，B，C的坐标分别为 $A (- 3 ， - 1)$ ， $B (- 2 ， - 4)$ ， $C (- 1 ， - 2)$ ．

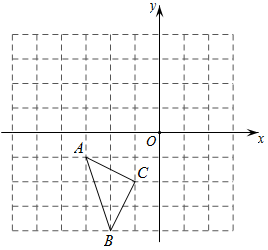(1)、先将 $△ A B C$ 沿y轴正方向平移3个单位长度，再沿x轴负方向平移1个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，点 $C_{1}$ 坐标是；

(2)、将 $△ A_{1} B_{1} C_{1}$ ，绕点 $B_{1}$ 逆时针旋转90°，得到 $△ A_{2} B_{1} C_{2}$ ，画出 $△ A_{2} B_{1} C_{2}$ ，点 $C_{2}$ 的坐标是．

(3)、我们发现点 $C$ ， $C_{2}$ 关于某点成中心对称，对称中心坐标是．

查看试题解析
22. 在 $△ A B C$ 中， $∠ B A C = 45 °$ ， $∠ A B C = 90 °$ ， $F$ 为 $A B$ 延长线上一点，点 $E$ 在 $B C$ 上，且 $A E = C F$ ．

(1)、求证： $R t △ A B E ≌ R t △ C B F$ ；

(2)、若 $∠ C A E = 30 °$ ，求 $∠ A C F$ 的度数．

查看试题解析
23. 如图，直线 $l_{1}$ ： $y = 2 x + 2$ 与 $x$ 轴交于A点，与y轴交于点C，直线 $l_{2}$ ： $y = k x + b$ 与x轴交于点 $B (3 ， 0)$ ，与y轴交于点E，与直线 $l_{1}$ 交于点D，且点D的纵坐标为4．

(1)、求不等式 $k x + b > 2 x + 2$ 的解集；

(2)、求直线 $l_{2}$ 的函数表达式；

(3)、求 $△ C D E$ 的面积．

查看试题解析
24. 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使BF＝BE，连接EC并延长，使CG＝CE，连接FG．H为FG的中点，连接DH．

(1)、求证：四边形AFHD为平行四边形；

(2)、若CB＝CE，∠BAE＝70°，∠DCE＝20°，求∠CBE的度数．

查看试题解析
25. 甲、乙两公司全体员工踊跃参与“携手防疫，共渡难关”捐款活动，甲公司共捐款100000元，乙公司共捐款140000元．下面是甲、乙两公司员工的一段对话：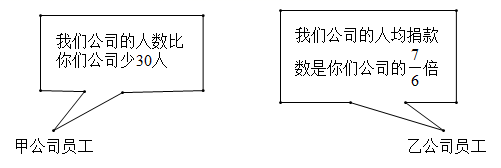

(1)、甲、乙两公司各有多少人？

(2)、现甲、乙两公司共同使用这笔捐款购买 $A$ 、 $B$ 两种防疫物资， $A$ 种防疫物资每箱15000元， $B$ 种防疫物资每箱12000元．若购买 $B$ 种防疫物资不少于10箱，并恰好将捐款用完，有几种购买方案？请设计出来（注： $A$ 、 $B$ 两种防疫物资均需购买，并按整箱配送）．

查看试题解析
26. 在某次数学兴趣小组延时服务课上，李老师要求学生探究如下问题：

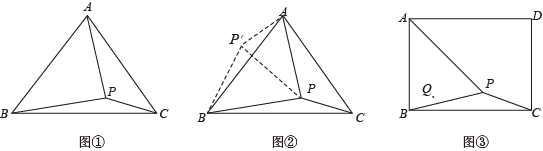(1)、如图①，在等边 $△ A B C$ 内有一点P， $P A = 2$ ， $P B = \sqrt{3}$ ， $P C = 1$ ．试求 $∠ B P C$ 的度数．小亮同学一时没有思路，当他认真分析题目信息后，发现以PA，PB，PC的长为边的三角形是直角三角形，他突然有了正确的思路：如图②，将 $△ B P C$ 绕点B逆时针旋转60°，得到 $△ B P^{'} A$ ，连接 $P P^{'}$ ，可求出 $∠ B P C$ 的度数，请你替小亮写出求解过程；

(2)、如图③，在正方形 $A B C D$ 内有一点 $P$ ， $P A = \sqrt{5}$ ， $P B = \sqrt{2}$ ， $P C = 1$ ．试求 $∠ B P C$ 的度数；

(3)、在图③中，若正方形 $A B C D$ 内有另一点Q， $Q A = a$ ， $Q B = b$ ， $Q C = c$ （ $a > b$ ， $a > c$ ）．请你探究：当a，b，c满足什么条件时， $∠ B Q C$ 的度数与第（2）问中 $∠ B P C$ 的度数相等，并说明理由．（友情提示：正方形的四条边都相等，四个角都是直角）

查看试题解析