江西省九江市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列几何图形中，既是轴对称图形，又是中心对称图形的是（　　）

A、等腰三角形 B、正三角形 C、平行四边形 D、正方形

查看试题解析
2. 计算 $\frac{1}{a} \div a$ 的结果为（）

A、a B、 $\frac{1}{a^{2}}$ C、1 D、 $a^{2}$

查看试题解析
3. 一个多边形的内角和为1800°，则这个多边形为（）

A、九边形 B、十边形 C、十一边形 D、十二边形

查看试题解析
4. 下列从左到右的变形是正确的因式分解的是（）

A、 $a x + a b = a (x + b)$ B、 $x^{4} - 1 = {(x + 1)}^{2} {(x - 1)}^{2}$ C、 $x^{2} - 4 x - 4 = {(x - 2)}^{2}$ D、 $x^{2} - y^{2} - 1 = (x + y + 1) (x - y - 1)$

查看试题解析
5. 不等式 $- \frac{1}{2} x > 1$ 的解集为（）

A、 $x > - 2$ B、 $x > - \frac{1}{2}$ C、 $x < - 2$ D、 $x < - \frac{1}{2}$

查看试题解析
6. 如图，在等边三角形 $A B C$ 中，点D是 $A C$ 边上的一点，连接 $B D$ ，将 $△ B C D$ 绕点B逆时针旋转60°，得到 $△ B A E$ ，连接 $E D$ ，若 $B C = a$ ， $B D = b$ ，则下列结论正确的有（）
① $A E ∥ B C$ ；② $∠ A D E = ∠ B D C$ ；③ $△ A D E$ 的周长等于 $(a + b)$ ；④ $△ B D E$ 是等边三角形

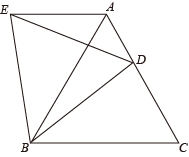A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析

二、填空题

7. 因式分解： $a^{2} - 1$ =.

查看试题解析
8. 命题“同位角相等，两直线平行”的逆命题是命题．（填“真”或“假”）

查看试题解析
9. 在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是

查看试题解析
10. 如图，一次函数 $y = - x + b$ 与 $y = k x - 1$ 的图象交于点P，与x轴交于点B．已知点P的纵坐标为3，点B的横坐标为4，则不等式 $- x + b > k x - 1$ 的解集为．

查看试题解析
11. $R t △ A_{1} B_{1} C_{1}$ 的两直角边 $A_{1} C_{1}$ ， $B_{1} C_{1}$ 的长分别是5，12，以 $△ A_{1} B_{1} C_{1}$ 三边的中点为顶点的三角形记为 $△ A_{2} B_{2} C_{2}$ ．以 $△ A_{2} B_{2} C_{2}$ 三边的中点为顶点的三角形记为 $△ A_{3} B_{3} C_{3}$ ．以此类推，则 $△ A_{5} B_{5} C_{5}$ 的周长为．

查看试题解析
12. 已知四边形 $A B C D$ ， $∠ B A D = 105 °$ ，对角线 $A C$ 将其分成两个三角形，其中 $△ A B C$ 是边长为2的等边三角形， $△ A C D$ 是等腰三角形，则 $A D$ 的长是．

查看试题解析

三、解答题

13.

(1)、因式分解： $2 m a^{2} + 4 m a b + m b^{2}$ ；

(2)、如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ，交 $A C$ 于点D，过点D作 $D E ∥ B C$ ，交 $A B$ 于点E．求证： $E B = E D$ ．

查看试题解析
14. 解方程： $\frac{1 - x}{x - 2}$ ＝ $\frac{1}{2 - x}$ ﹣2.

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，垂足为D，E为 $A C$ 上一点， $B E$ 交 $A D$ 于点F，且 $B F = A C$ ， $F D = C D$ ， $A D = 2$ ，求 $A B$ 的长．

查看试题解析
16. 求不等式组 ${\begin{array}{l} x - 3 (x - 2) < 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ 的解集，并将解集画在数轴上．

查看试题解析
17.
⑴在平面直角坐标系中描出点 $A (- 3 ， - 4)$ ， $B (- 2 ， - 2)$ ， $C (1 ， - 3)$ ，得到 $△ A B C$ ．

⑵将（1）中的 $△ A B C$ 先向右平移4个单位，再向上平移3个单位．画出平移后的 $△ A^{'} B^{'} C^{'}$ ．

⑶请说明如何将 $△ A^{'} B^{'} C^{'}$ 看成是 $△ A B C$ 经过一次平移得到的．

查看试题解析
18. 先化简，再求值： $(\frac{2 x}{x^{2} - 1} - \frac{1}{x - 1}) \div \frac{x}{x + 1}$ ，其中整数 $x$ 满足不等式 $- 1 \leq x \leq 2$ ．

查看试题解析
19. 某商家用3000元购买了一种商品，面市后供不应求，第二次又用5400元购买了这种商品，所购商品的数量比第一次多50件，但单价涨了20%．若销售这种商品每件定价都是50元，所有商品全部售完后，商家共赢利多少元？

查看试题解析
20. 如图，点P是等边三角形 $△ A B C$ 外一点， $P A = 2 \sqrt{2}$ ， $P B = 1$ ， $P C = 3$ ．将 $△ P B C$ 绕点B逆时针旋转60°后得到 $△ D B A$ ．

(1)、求证： $△ P D A$ 是直角三角形；

(2)、求 $△ A P B$ 的面积．

查看试题解析
21. 暑假期间，两位家长计划带领若干名学生去旅游，他们联系了报价均为每人500元的两家旅行社．经协商，甲旅行社的优惠条件是：两位家长全额收费，学生都按照七折收费；乙旅行社的优惠条件是：家长、学生都按照八折收费．

(1)、设参加旅游的学生有x人，甲、乙旅行社的总价分别为 $y_{1}$ ， $y_{2}$ 元，请列出 $y_{1}$ ， $y_{2}$ 关于x的函数关系式；（不用写出自变量的取值范围）

(2)、他们应该选择哪家旅行社？

查看试题解析
22. 如图，点M是 $△ A B C$ 的边 $A B$ 上一点，连接 $C M$ ，过A作 $A D ⊥ C M$ 于点 $D$ ，过B作 $B E ⊥ C M$ 于点E．

(1)、如图①，若点M为 $A B$ 的中点时，连接 $A E$ ， $B D$ ，求证：四边形 $A D B E$ 是平行四边形；

(2)、如图②，若点M不是 $A B$ 的中点，点O是 $A B$ 上不与M重合的一点，连接 $D O$ ， $E O$ ，已知点O在 $D E$ 的垂直平分线上，求证： $A O = B O$ ．

查看试题解析
23. 已知点 $A (0 ， - 2)$ ，点B为x正半轴上的一个动点，连接 $A B$ ，将 $A B$ 绕点A逆时针旋转一个角度 $α$ （ $0 < α \leq 90 °$ ）得到线段 $A C$ ．设点C的坐标为 $(x ， y)$ ．

(1)、如图①，若 $∠ α = 90 °$ ，过点C向y轴作 $C D ⊥ y$ 轴于点D，则 $△ A C D$ 与 $△ B A O$ 的关系是，由此可知点C的横坐标为；

(2)、如图②，若 $∠ α = 45 °$ ，
①当点B运动到 $B_{0}$ 时，旋转后的对应点 $C_{0}$ 恰好落在y轴上，则点 $B_{0}$ 的坐标为 ▲ ，点 $C_{0}$ 的坐标为 ▲ ；
②当点B离开 $B_{0}$ 向右边移动时，点C同时离开 $C_{0}$ ，连接 $C C_{0}$ ，证明 $△ A C C_{0} ≌ △ A B B_{0}$ ，并求出点 $C$ 的坐标 $y$ 与 $x$ 的函数关系式；

(3)、如图③，请直接写出当 $∠ α = 60 °$ 时点 $C$ 的坐标 $y$ 与 $x$ 的函数关系．

查看试题解析