黑龙江省哈尔滨市香坊区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x^{2} - \frac{2}{x} = 0$ B、 $3 x + 1 = 7 x$ C、 $a^{2} - 2 a = 0$ D、 $2 x - 5 = y$

查看试题解析
2. 下列四边形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列曲线中表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
4. 若正比例函数 $y = k x (k \neq 0)$ 的图象经过点 $(1 ， 3)$ ，则k的值为（）

A、3 B、 $\frac{1}{3}$ C、 $- 3$ D、 $- \frac{1}{3}$

查看试题解析
5. 下列各组数中，能作为直角三角形三边长的是（）

A、1，4，9 B、5，12，13 C、5，6，7 D、5，11，12

查看试题解析
6. 一元二次方程 $x^{2} - 4 x + 2 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
7. 下列命题正确的是（）

A、对角线互相垂直的四边形是菱形 B、有两条边相等的四边形是平行四边形 C、有三个角是直角的四边形是矩形 D、四条边都相等的平行四边形是正方形

查看试题解析
8. 如图，▱ABCD的周长为20cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（　　）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
9. 如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位： $m m$ ），可以计算出两圆孔中心B和C的距离为（） $m m$ ．

A、120 B、135 C、 $30 \sqrt{61}$ D、150

查看试题解析
10. A、B两地在一条笔直的公路上，甲从A地出发前往B地、乙从B地出发前往A地．两人同时出发，甲到达B地后停止，乙继续前进到达A地，下图表示两人的距离y（米）与时间x（分）间的函数关系，则下列结论中正确的个数有（       ）
①A、B两地的距离是1200米       ②两人出发4分钟相迎
③甲的速度是100米/分       ④乙出发12分钟到达A地

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 函数 $y = \frac{3}{x - 2}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
12. 已知 $x = 1$ 是方程 $3 x^{2} - 2 x + m = 0$ 的一个根．则m的值是．

查看试题解析
13. 某公司3月份的利润为200万元，5月份的利润为242万元，则平均每月利润的增长率是．

查看试题解析
14. 在平面直角坐标系中，已知一次函数 $y = - \frac{1}{2} x + 2$ 的图像经过 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 两点，若 $x_{1} < x_{2}$ ，则 $y_{1}$ $y_{2}$ ．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看试题解析
15. 如图，在▱ABCD中，BC=18，AB=15，BE平分∠ABC，交AD于点E，则ED= ．

查看试题解析
16. 函数 $y = k x + b (k \neq 0)$ 的图象如图所示，则关于x的不等式 $k x + b > 0$ 的解集为．

查看试题解析
17. 如图，在菱形 $A B C D$ 中， $∠ A = 120 °$ ，对角线 $B D$ 的长为3，则菱形的边长为．

查看试题解析
18. 在一次聚会中，每两人都握了一次手，所有人共握手15次，有人参加聚会．

查看试题解析
19. 已知矩形 $A B C D$ 中， $A B = 2$ ， $B C = 4$ ，点E在直线 $C D$ 上， $D E = 1$ ．则线段 $B E$ 的长为．

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 12$ ， $B C = 5$ ，点D在 $△ A B C$ 外，连接 $A D$ 、 $B D$ ，点E是 $B D$ 的中点， $A D = 4$ ， $∠ C A D = ∠ C A B$ ，则线段 $C E$ 的长．

查看试题解析

三、解答题

21. 解方程：

(1)、 ${(x - 1)}^{2} - 4 = 0$

(2)、 ${(x - 2)}^{2} = 3 x - 6$

查看试题解析
22. 如图，在边长为1的小正方形组成的 $8 \times 12$ 的网格中，给出了以格点（网格线的交点）为端点的线段 $A B$ ， $E F$ ．

⑴在图中画出以 $A B$ 为边的 $▱ A B C D$ ，使 $∠ B A D$ 为钝角，平行四边形周长为 $6 + 4 \sqrt{5}$ ；

⑵在图中画出以 $E F$ 为边的菱形 $E F G H$ ，使其面积为20；

⑶连接 $D H$ ，请直接写出线段 $D H$ 的长．

查看试题解析
23. 如图，在平面直角坐标系中，点O为坐标原点，直线 $B C$ 交y轴于点B，交x轴于点C，B点坐标为 $(0 ， 4)$ ， $O B = O C$ ．

(1)、求直线 $B C$ 的解析式；

(2)、若 $△ A B O$ 的面积为2，求A点坐标．

查看试题解析
24. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ，点F是 $A D$ 边的中点，连接 $B F$ 并延长交 $C D$ 的延长线于点E， $C D = D E$ ．

(1)、如图1，求证：四边形 $A B C D$ 为平行四边形；

(2)、如图2，过点D作 $D G ∥ B F$ 交 $B C$ 于点G，连接 $F G$ ，在不添加任何辅助线的情况下，请直接写出图中的所有平行四边形（ $▱ A B C D$ 除外）．

查看试题解析
25. 如图，在矩形 $A B C D$ 的场地内，修建横竖两条甬道，场地其余部分种植草评，已知竖向甬道的宽度是横向甬道宽度的2倍， $A D = 20$ 米， $A B = 16$ 米，设横向甬道的宽度为x米，草坪面积为y米² ．

(1)、请写出y与x之间的函数关系式；（不必写出自变量的取值范围）

(2)、若草坪面积为270米² ，请求出横向甬道的宽度．

查看试题解析
26. 已知：四边形 $A B C D$ 是平行四边形，点E是 $A B$ 边的中点，连接 $D E$ ，过点A作 $A F ⊥ D E$ ，垂足为点G，交 $B C$ 边于点F，点H是线段 $G F$ 上一点，连接 $B H$ ， $D H$ ， $D H = B C$ ．

(1)、如图1，求证： $B H ∥ D E$ ；

(2)、如图2，延长 $B H$ 交C $D$ 边于点K，连接 $F K$ ，若 $D H ∥ F K$ ，求证： $B H = H K$ ；

(3)、如图3，在（2）的条件下，连接 $K E$ ，延长 $K E$ 至点M，连接 $A M$ 、 $B M$ ，若 $∠ A M B = 135 °$ ， $A D = \sqrt{5} A E$ ， $B K = 2 \sqrt{10}$ ，求 $A M$ 的长．

查看试题解析
27. 已知：在平面直角坐标系中，点O为坐标原点，直线 $y = - \frac{4}{3} x + 8$ 交x轴于点A，交y轴于点B，点D是x轴负半轴上一点，四边形 $A B C D$ 是菱形．

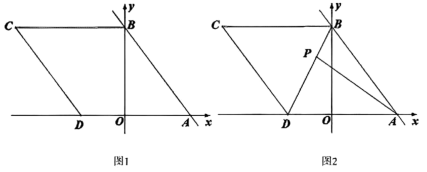
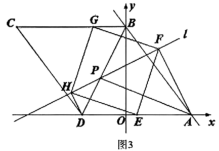(1)、如图1，求D点坐标；

(2)、如图2，连接 $B D$ ，点P是线段 $B D$ 上一点（点P不与点B、点D重合），连接 $A P$ ，设P点横坐标为t， $△ A D P$ 的面积为S，求S与t之间的函数关系式（不要求写出自变量t的取值范围）；

(3)、如图3，在（2）的条件下，直线l经过点P，过点A、点D分别作直线l的垂线，垂足分别为点F、点H，点E是线段 $A D$ 的中点，点G是线段 $B C$ 上一点，连接 $E F$ 、 $F G$ 、 $G H$ 、 $H E$ ，当四边形 $E F G H$ 是矩形时，求 $△ A D P$ 的面积．

查看试题解析