黑龙江省大庆市肇源县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 某班级第组第排位置可以用数对表示,则数对表示的位置是( )A、第组第排 B、第组第排 C、第组第排 D、第组第排3. 直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )A、6cm B、8cm C、 cm D、 cm4. 若函数是一次函数,则m的值为 ( )A、1 B、-1 C、1 D、25. 实数x,y满足方程组 , 则的值为( )A、3 B、-5 C、5 D、-36. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、57. 如图,点 在 的延长线上, 于点 ,交 于点 .若 ,则 的度数为( ).
 A、65° B、70° C、75° D、85°8. 若a满足 , 则a的值为( )A、1 B、0 C、0或1 D、0或1或9. 一个两位数,十位上的数与个位上的数之和是7,如果把这个两位数加上9,所得的两位数的个位数字,十位数字恰好分别是原来两位数的十位数字和个位数字,则这个两位数是( )A、34 B、43 C、25 D、5210. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
A、65° B、70° C、75° D、85°8. 若a满足 , 则a的值为( )A、1 B、0 C、0或1 D、0或1或9. 一个两位数,十位上的数与个位上的数之和是7,如果把这个两位数加上9,所得的两位数的个位数字,十位数字恰好分别是原来两位数的十位数字和个位数字,则这个两位数是( )A、34 B、43 C、25 D、5210. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )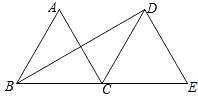 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,点关于原点对称的点的坐标是 .12. 当a=时,最简二次根式与是同类二次根式.13. (x+y-5)2+=0 则点p(x,y)在第象限.14. 甲、乙、丙、丁四人参加滑雪比赛,经过三轮初赛,他们的平均成绩相同,方差分别是 , , , , 你认为成绩更稳定的是 .15. 如图,直线 : 与直线 : 相交于点P(m,4),则方程组 的解是 .
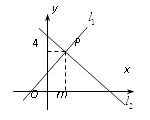 16. 如图,把一块含有角的直角三角板放置在两条平行线上,若 , 则的度数为 .
16. 如图,把一块含有角的直角三角板放置在两条平行线上,若 , 则的度数为 . 17. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:中, , , , 则的长为 .18. 已知一次函数的图象经过点 , 与x轴的交点为B,若 , 则这个一次函数的解析式为 .
17. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:中, , , , 则的长为 .18. 已知一次函数的图象经过点 , 与x轴的交点为B,若 , 则这个一次函数的解析式为 .三、解答题
-
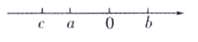
19. 计算:(1)、(2)、20. 用适当的方法解下列方程组:(1)、;(2)、 .21. 已知实数a,b,c在数轴上的位置如图所示,化简: .
 22. 如图所示,在平面直角坐标系中,已知 、 、 .
22. 如图所示,在平面直角坐标系中,已知 、 、 . (1)、在平面直角坐标系中画出 ,则 的面积是;(2)、若点D与点C关于y轴对称,则点D的坐标为;(3)、已知P为x轴上一点,若 的面积为4,求点P的坐标.23. 如图,四边形中,已知 , , , , 且 .
(1)、在平面直角坐标系中画出 ,则 的面积是;(2)、若点D与点C关于y轴对称,则点D的坐标为;(3)、已知P为x轴上一点,若 的面积为4,求点P的坐标.23. 如图,四边形中,已知 , , , , 且 . (1)、求的大小;(2)、求四边形的面积;24. 甲、乙两位学生参加校运会射击选拔赛,两人各射击了5次,小明根据他们的成绩(单位:环)列表,并计算了甲成绩的平均数和方差(见小明的作业).
(1)、求的大小;(2)、求四边形的面积;24. 甲、乙两位学生参加校运会射击选拔赛,两人各射击了5次,小明根据他们的成绩(单位:环)列表,并计算了甲成绩的平均数和方差(见小明的作业).甲、乙两人射击成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
4
7
小明的作业
解:=×(9+4+7+4+6)=6,
S甲2=×[(9﹣6)2+(4﹣6)2+(7﹣6)2+(4﹣6)2+(6﹣6)2]
=×(9+4+1+4+0)
=3.6
(1)、请参照小明的计算方法,求出乙成绩的平均数与方差.(2)、请你从平均数和方差的角度分析,谁将被选中.25. 若关于x,y的方程组 与 有相同的解.
(1)、求这个相同的解;(2)、求m,n的值.
26. 现有一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,为节约成本,每辆货车均装满.已知过去两次租用这两种货车的运货情况如下表所示:第一次
第二次
甲种货车辆数(单位:辆)
2
5
乙种货车辆数(单位:辆)
3
6
该次运货物吨数(单位:吨)
17
38
(1)、求甲、乙两种货车每辆可装多少吨货物?(2)、现租用该公司3辆甲种货车及4辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?

