河北省廊坊市安次区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 下列式子一定是二次根式的是( )A、 B、 C、 D、2. 三角形边长分别为下列各数,其中能围成直角三角形的是 ( )A、2,3,4 B、3,4,5 C、4,5,6 D、5,6,73. 在函数中,的值是( )A、3 B、 C、6 D、4. 已知正比例函数 的图象经过点 则k的值为( )A、 B、 C、 D、5. 如图,为了测量一块不规则绿地B,C两点间的距离,可以在绿地的一侧选定一点A,然后测量出AB,AC的中点D,E,如果测量出D,E两点间的距离是8m,那么绿地B,C两点间的距离是( )
 A、4m B、8m C、16m D、20m6. 下列各曲线中,不表示y是 x的函数的是( )A、
A、4m B、8m C、16m D、20m6. 下列各曲线中,不表示y是 x的函数的是( )A、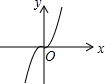 B、
B、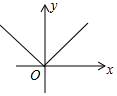 C、
C、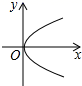 D、
D、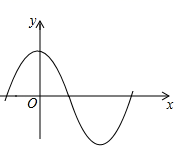 7. 如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1 , S2 , 若S1=8cm2 , S2=17cm2 , 则斜边AB的长是( )
7. 如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1 , S2 , 若S1=8cm2 , S2=17cm2 , 则斜边AB的长是( ) A、3cm B、6cm C、4cm D、5cm8. 下列运算正确的是( )A、 B、 C、=6 D、÷=39. 如图,直线y=kx+b与x轴的交点的坐标是(﹣3,0),那么关于x的不等式kx+b>0的解集是( )
A、3cm B、6cm C、4cm D、5cm8. 下列运算正确的是( )A、 B、 C、=6 D、÷=39. 如图,直线y=kx+b与x轴的交点的坐标是(﹣3,0),那么关于x的不等式kx+b>0的解集是( ) A、x>﹣3 B、x<﹣3 C、x>0 D、x<010. 在菱形ABCD中,对角线AC,BD相交于点O,如果AC=6,BD=8,那么菱形ABCD的面积是( )A、6 B、12 C、24 D、4811. 以2022年北京冬奥会为契机,某学校开展以“弘扬奥林匹克精神,感受冰雪运动魅力”为主题的冰雪嘉年华实践课程.为了解学生掌握滑雪技巧及滑雪水平等情况,教练分别对甲、乙两名学生10次训练的结果进行了统计,其中每次训练的成绩分别为5分,4分,3分,2分,1分五档.统计结果如图所示,下列结论正确的是( )
A、x>﹣3 B、x<﹣3 C、x>0 D、x<010. 在菱形ABCD中,对角线AC,BD相交于点O,如果AC=6,BD=8,那么菱形ABCD的面积是( )A、6 B、12 C、24 D、4811. 以2022年北京冬奥会为契机,某学校开展以“弘扬奥林匹克精神,感受冰雪运动魅力”为主题的冰雪嘉年华实践课程.为了解学生掌握滑雪技巧及滑雪水平等情况,教练分别对甲、乙两名学生10次训练的结果进行了统计,其中每次训练的成绩分别为5分,4分,3分,2分,1分五档.统计结果如图所示,下列结论正确的是( ) A、 , B、 , C、 , D、 ,12. 如图,在M、N、P、Q四个点中,一次函数 , 若 , , 则图象不可能经过的点是( )
A、 , B、 , C、 , D、 ,12. 如图,在M、N、P、Q四个点中,一次函数 , 若 , , 则图象不可能经过的点是( ) A、点M B、点N C、点P D、点Q13. 如图,E是平行四边形边上一点,且 , 连接 , 并延长与的延长线交于点F,如果 , 那么的度数是( )
A、点M B、点N C、点P D、点Q13. 如图,E是平行四边形边上一点,且 , 连接 , 并延长与的延长线交于点F,如果 , 那么的度数是( ) A、30° B、40° C、50° D、70°14. 已知四边形ABCD是平行四边形,下列结论错误的是( )A、当时,它是菱形 B、当时,它是菱形 C、当时,它是矩形 D、当时,它是正方形15. 关于一次函数 , 下列说法:
A、30° B、40° C、50° D、70°14. 已知四边形ABCD是平行四边形,下列结论错误的是( )A、当时,它是菱形 B、当时,它是菱形 C、当时,它是矩形 D、当时,它是正方形15. 关于一次函数 , 下列说法:①当时,图象从左向右上升,y随x的增大而增大;
②当时,图象经过第二、三、四象限;
③函数图象一定过点 .
其中正确的是( )
A、①② B、①③ C、②③ D、①②③16. 已知:如图所示:点D,E分别是的边 , 的中点.求证: , 且 .

证明:延长到点F,使 , 连接 , , .
,
四边形是平行四边形,
接着以下是排序错误的证明过程:
①;
② , 即;
③四边形是平行四边形;
④ , 且 .
则正确的证明顺序应是( )
A、①→③→②→④ B、①→③→④→② C、②→③→①→④ D、②→③→④→①二、填空题
-
17. 若代数式在实数范围内有意义,则的取值范围是 .18. 如图,矩形ABCD的对角线AC、BD相交于点O,OA=3,则BD的长为 .
 19. 甲乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙先骑共享自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米.图中的折线表示甲乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,根据图像可知:甲步行速度为米/分;乙骑自行车的速度为米/分;乙到还车点时,甲乙两人相距米.
19. 甲乙两位同学住在同一小区,学校与小区相距2700米,一天甲从小区步行出发去学校,12分钟后乙先骑共享自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快5米.图中的折线表示甲乙两人之间的距离y(米)与甲步行时间x(分钟)的函数关系图像,根据图像可知:甲步行速度为米/分;乙骑自行车的速度为米/分;乙到还车点时,甲乙两人相距米.
三、解答题
-
20. 某工厂有一个容积为280立方米的水池,现用3台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时抽水15立方米.(1)、抽水两个小时后,池中还有水立方米;(2)、在这一变化过程中哪些是变量?哪些是常量?21. 计算:(1)、;(2)、 .22. “疫情远未结束,防疫绝不放松”.为了了解同学们掌握防疫知识的情况,增强防疫意识,某校举行了疫情防护知识测试活动,现从该校七、八年级各随机抽取20名学生的测试成绩(90分及以上为优秀)进行整理、描述和分析,以下是部分信息.
七年级20名学生的测试成绩:72,80,85,90,78,82,80,90,92,90,100,90,83,88,97,98,99,80,81,85.
八年级20名学生的测试成绩条形统计图如图:

【七、八年级抽取的学生的测试成绩的平均数、众数、中位数、90分及以上人数所占百分比如下表所示】:
年级
平均数
众数
中位数
90分及以上人数所占百分比
七年级
87
a
86.5
45%
八年级
87
94
b
c
根据以上信息,解答下列问题:
(1)、a=、b=、c=;(2)、根据上述数据,你认为该校七、八年级中,哪个年级掌握防疫知识更好?请说明理由;(3)、该校七、八年级共有3000名学生参加了此次测试活动,估计参加此次测试活动成绩优秀的学生有多少人?23. 如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .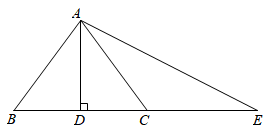 (1)、求证: ;(2)、若 , ,求 的周长和面积.24. 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1),与y轴的交点为C,与x轴的交点为D.
(1)、求证: ;(2)、若 , ,求 的周长和面积.24. 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1),与y轴的交点为C,与x轴的交点为D. (1)、求一次函数解析式;(2)、求C点的坐标;(3)、求△AOD的面积.25. 学校组织暑期夏令营,学校联系了报价均为每人200元的两家旅行社,经协商,甲旅行社的优惠条件是:全部师生7.5折优惠;乙旅行社的优惠条件是:可免去一位老师的费用,其余师生8折优惠.(1)、分别写出两家旅行社所需的费用(元)与师生人数(人)的函数关系式;(2)、请你通过计算判断学校应选择哪家旅行社?26. 如图,用硬纸板剪一个平行四边形ABCD,找到对角线交点O,用大头针在点O处将一根平放在平行四边形上的细直木条固定,并使细木条可以绕点O转动,拨动细木条,可随意停留在任意位置.
(1)、求一次函数解析式;(2)、求C点的坐标;(3)、求△AOD的面积.25. 学校组织暑期夏令营,学校联系了报价均为每人200元的两家旅行社,经协商,甲旅行社的优惠条件是:全部师生7.5折优惠;乙旅行社的优惠条件是:可免去一位老师的费用,其余师生8折优惠.(1)、分别写出两家旅行社所需的费用(元)与师生人数(人)的函数关系式;(2)、请你通过计算判断学校应选择哪家旅行社?26. 如图,用硬纸板剪一个平行四边形ABCD,找到对角线交点O,用大头针在点O处将一根平放在平行四边形上的细直木条固定,并使细木条可以绕点O转动,拨动细木条,可随意停留在任意位置. (1)、木条把平行四边形ABCD分成了两部分,在拨动细木条的过程中,两部分的面积是否始终相等?答:(填“是”或“否”);(2)、木条与▱ABCD的边AD,BC相交于点E,F.
(1)、木条把平行四边形ABCD分成了两部分,在拨动细木条的过程中,两部分的面积是否始终相等?答:(填“是”或“否”);(2)、木条与▱ABCD的边AD,BC相交于点E,F.①请判断OE与OF是否始终相等,并说明理由;
②以A,E,C,F为顶点的四边形是平行四边形吗?为什么?