广东省惠州市仲恺高新区2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2022-07-22 类型:期末考试
一、单选题
-
1. 二次根式中的x取值范围是( )A、x≥-3 B、x≥3 C、x≥0 D、x≤-32. 汽车由A地驶往相距120km的B地,它的平均速度是60km/h,则汽车距B地路程s(km)与行驶时间t(h)的关系式为( ).A、 B、 C、 D、3. 下列根式中属于最简二次根式的是( )A、 B、 C、 D、4. 下列各组数中,是勾股数的为( )A、1,1, B、5,12,13 C、1.5,2,2.5 D、7,8,95. 已知菱形ABCD的对角线AC=2,BD=4,则菱形ABCD的面积是( ).A、 B、4 C、 D、86. 如图,四边形ABCD是矩形,E,F,G,H分别为各边的中点,则四边形EFGH一定是( )
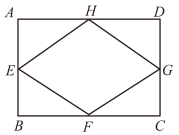 A、菱形 B、矩形 C、正方形 D、对角线相等的四边形7. 如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( ).
A、菱形 B、矩形 C、正方形 D、对角线相等的四边形7. 如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( ).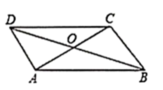 A、∠ADB=∠CBD B、AD=OD C、AO=OC D、8. 已知点 、 在函数 的图象上,当 时, ,则该函数的图象大致是( )A、
A、∠ADB=∠CBD B、AD=OD C、AO=OC D、8. 已知点 、 在函数 的图象上,当 时, ,则该函数的图象大致是( )A、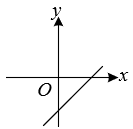 B、
B、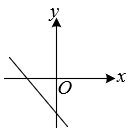 C、
C、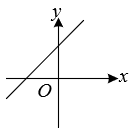 D、
D、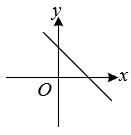 9. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )
9. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )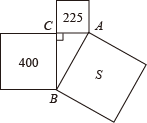 A、25 B、175 C、600 D、62510. 如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,点P为边AB上一点,且点P不与点A,B重合.过点P作于点E,于点F,连接EF,则EF的最小值为( )
A、25 B、175 C、600 D、62510. 如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,点P为边AB上一点,且点P不与点A,B重合.过点P作于点E,于点F,连接EF,则EF的最小值为( )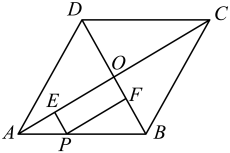 A、2 B、2.4 C、2.5 D、3
A、2 B、2.4 C、2.5 D、3二、填空题
-
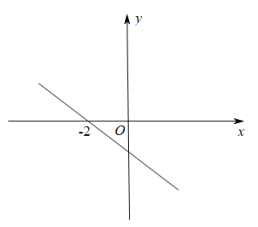
11. 若函数的图象经过第二、四象限,则k的取值范围是 .12. 比较大小:13. 2022年冬季奥运会将在北京和张家口举办,北京将成为世界上第一个既举办过夏季奥运会,又举办过冬季奥运会的城市.备战此次冬季奥运会,甲、乙两名运动员练习投掷实心球,每人投10次.若两人的平均成绩相同,方差分别为=0.13,=0.02,则成绩比较稳定的是(填“甲”或“乙”)运动员.14. 一次函数y=kx+b(k,b为常数且k≠0)的图象如图所示,且经过点(-2,0),则关于x的不等式kx+b>0的解集为
 15. 如图,在中, . 将折叠,使点B恰好落在边上,与点重合,为折痕,则的周长为 .
15. 如图,在中, . 将折叠,使点B恰好落在边上,与点重合,为折痕,则的周长为 .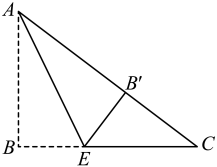 16. 如图,在△ABC中,D,E分别为AB,AC的中点,点F在线段DE上,且AF⊥BF.若AB=4,BC=7,则EF的长为 .
16. 如图,在△ABC中,D,E分别为AB,AC的中点,点F在线段DE上,且AF⊥BF.若AB=4,BC=7,则EF的长为 . 17. 如图1,四边形是平行四边形,连接 , 动点P从点A出发沿折线匀速运动,回到点A后停止.设点P运动的路程为x,线段的长为y,图2是y与x的函数关系的大致图象,则的面积为 .
17. 如图1,四边形是平行四边形,连接 , 动点P从点A出发沿折线匀速运动,回到点A后停止.设点P运动的路程为x,线段的长为y,图2是y与x的函数关系的大致图象,则的面积为 .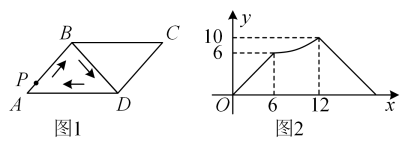
三、解答题
-
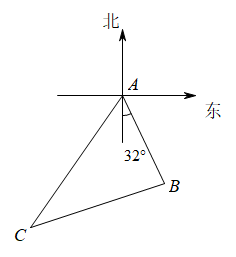
18. 计算:19. 已知y是关于x的一次函数,且当时,;当时, .(1)、求该一次函数的表达式;(2)、当时,求自变量的值.20. 某船从港口A出发沿南偏东32°方向航行12海里到达B岛,然后沿某方向航行16海里到达C岛,最后沿某个方向航行了20海里回到港口A,则该船从B到C是沿哪个方向航行的?(即求C岛在B岛的哪个方位,距离B岛多远?),请说明理由.
 21. 2月20日,北京冬奥会圆满落幕.在这届举世瞩目的冬奥会中,谷爱凌“一飞冲天”,苏翊鸣“一鸣惊人”,短道速滑梦之队“一往无前”…运动健儿们挑战极限、攀登顶峰的精神鼓舞着无数人.为弘扬奥运精神,培养学生对体育的热爱,某校随机抽取名学生,进行“奥运知识知多少”的测试,满分分,并绘制如下统计图:
21. 2月20日,北京冬奥会圆满落幕.在这届举世瞩目的冬奥会中,谷爱凌“一飞冲天”,苏翊鸣“一鸣惊人”,短道速滑梦之队“一往无前”…运动健儿们挑战极限、攀登顶峰的精神鼓舞着无数人.为弘扬奥运精神,培养学生对体育的热爱,某校随机抽取名学生,进行“奥运知识知多少”的测试,满分分,并绘制如下统计图: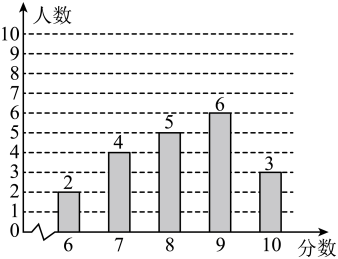 (1)、这名学生成绩的中位数是 , 众数是;(2)、求这名学生成绩的平均数;(3)、若成绩在9分及以上为优秀,请你估计该校名学生中,成绩为优秀的学生有多少名?22. 如图,已知Rt△ABC中,∠C=90°,AC , BC , 求:
(1)、这名学生成绩的中位数是 , 众数是;(2)、求这名学生成绩的平均数;(3)、若成绩在9分及以上为优秀,请你估计该校名学生中,成绩为优秀的学生有多少名?22. 如图,已知Rt△ABC中,∠C=90°,AC , BC , 求: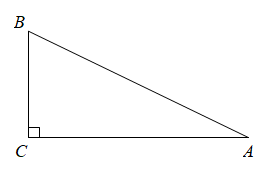 (1)、Rt△ABC的面积;(2)、求斜边AB上的高.23. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是边AC、AB的中点,连接CE、DE,过D点作DF∥CE交BC的延长线于F点.
(1)、Rt△ABC的面积;(2)、求斜边AB上的高.23. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是边AC、AB的中点,连接CE、DE,过D点作DF∥CE交BC的延长线于F点.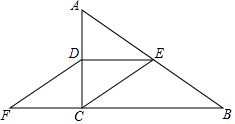 (1)、证明:四边形DECF是平行四边形;(2)、若AB=13cm,AC=5cm,求四边形DECF的周长.24. 如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D.
(1)、证明:四边形DECF是平行四边形;(2)、若AB=13cm,AC=5cm,求四边形DECF的周长.24. 如图,直线l:y=x+b过点A(﹣3,0),与y轴交于点B,∠OAB的平分线交y轴于点C,过点C作直线AB的垂线,交x轴于点E,垂足是点D. (1)、求点B和点C的坐标;(2)、求直线DE的函数关系式;(3)、设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.25. 综合与实践
(1)、求点B和点C的坐标;(2)、求直线DE的函数关系式;(3)、设点P是y轴上一动点,当PA+PD的值最小时,请直接写出点P的坐标.25. 综合与实践在数学教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动——折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.
实践发现:
对折矩形纸片ABCD,使AD与BC重合,折痕为EF,把纸片展平:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,折痕为BM,把纸片展平,连接AN,如图①;
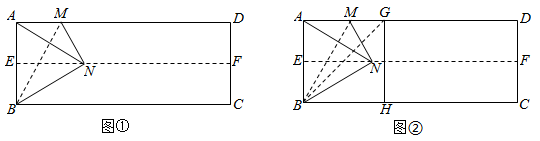
 (1)、折痕BM所在直线是否是线段AN的垂直平分线?请判断图中是什么特殊三角形?请写出解答过程.(2)、继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,求∠GBN的度数.(3)、拓展延伸:
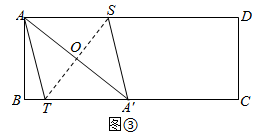
(1)、折痕BM所在直线是否是线段AN的垂直平分线?请判断图中是什么特殊三角形?请写出解答过程.(2)、继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,求∠GBN的度数.(3)、拓展延伸:如图③,折叠矩形纸片ABCD,使点A落在BC边上的点处,并且折痕交BC边于点T,交AD边于点S,把纸片展平,连接交ST于点O,连接AT;求证:四边形是菱形.