广东省广州市海珠区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 3}$ 有意义，则x的取值范围是（）．

A、 $x > 3$ B、 $x < 3$ C、 $x \geq 3$ D、 $x \leq 3$

查看试题解析
2. 下列各图像中，y不是x的函数的是（）．

A、 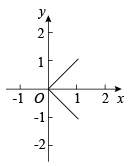B、 C、 D、

查看试题解析
3. 下列计算正确的是（）．

A、 $\sqrt{6} \div \sqrt{3} = 2$ B、 $\sqrt{8} - \sqrt{3} = \sqrt{5}$ C、 ${(2 \sqrt{5})}^{2} = 20$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
4. 如图所示，在 $▱ A B C D$ 中， $D E ⊥ B C$ ，垂足为E，如果 $∠ A = 72 °$ ，则 $∠ C D E$ 度数是（）．

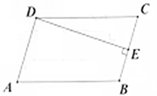A、18° B、20° C、22° D、28°

查看试题解析
5. 一次函数 $y = 2 x - 3$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 以下列各组数作为边长，①16，20，12；②25，7，24；③12，13，5；④16，8，15，能组成直角三角形的有（）．

A、1组 B、2组 C、3组 D、4组

查看试题解析
7. 甲、乙、丙、丁四人进行射击测试，记录每人10次射击成绩，得到各人的射击成绩平均数和方差如表中所示，则成绩最稳定的是（）
统计量
甲
乙
丙
丁
平均数
$9.2$
$9.2$
$9.2$
$9.2$
方差
$0.60$
$0.62$
$0.50$
$0.44$

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 将直线 $y = x + 1$ 向下平移2个单位，得到直线（）．

A、 $y = x - 2$ B、 $y = - x + 1$ C、 $y = - x - 1$ D、 $y = x - 1$

查看试题解析
9. 下列命题是假命题的是（）．

A、直线 $y = x + 4$ 与y轴交于点 $(0 ， 4)$ B、在一次函数 $y = - 2 x + 3$ 中，y随着x的增大而增大 C、矩形的对角线相等 D、若 $\sqrt{x - 2} + \sqrt{y + 3} = 0$ ，则 $x + y = - 1$

查看试题解析
10. 如图，在四边形ACBD中，AD=BD，∠ADB=120°，点C为动点，∠ACB=90°，E是BD的中点，连接CE，当CE的长度最大时，此时∠CAB的大小是（）．

A、30° B、45° C、60° D、75°

查看试题解析

二、填空题

11. 正比例函数 $y = k x$ （ $k \neq 0$ ）的图象过点（-1，3），则k=.

查看试题解析
12. Rt△ABC中，三边分别是a，b，c，斜边c=3，则a²+b²+c²的值为．

查看试题解析
13. 某班共有50名学生，平均身高166cm，其中30名男生的平均身高为170cm，则20名女生的平均身高为cm．

查看试题解析
14. 如图，正方形ABCD被分成两个小正方形和两个长方形，如果两个小正方形的面积分别是 $8 c m^{2}$ 和 $3 c m^{2}$ ，那么两个长方形的面积为 $c m^{2}$ ．

查看试题解析
15. 在 $△ A B C$ 中， $A B = 13$ ， $B C = 10$ ， $B C$ 边上的中线 $A D = 12$ ，则 $A C$ 的长为．

查看试题解析
16. 如图，在7×7的正方形网格中，A，B两点是格点，如果点C也是格点，且△ABC是等腰三角形，这样的C点有个．

查看试题解析

三、解答题

17. 如图，已知四边形ABCD中， $A B = D C$ ，点E在BC的延长线上， $∠ A + ∠ B = 180 °$ ， $∠ A + ∠ D C E = 180 °$ ，求证：四边形ABCD是平行四边形．

查看试题解析
18. 计算：

(1)、 $\sqrt{3} - \sqrt{4^{2}} + 6 \times \sqrt{\frac{1}{3}}$ ；

(2)、 $(\sqrt{50} - \sqrt{3} \times \sqrt{6}) \div \sqrt{2}$ ．

查看试题解析
19. 小李是社区宣传干事，为宣传节约用水，他随机调查了某小区部分家庭6月份的用水情况，并将收集的数据整理成如下的统计图．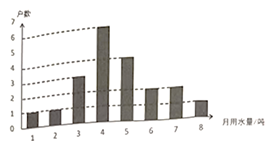

(1)、小李调查了户家庭；

(2)、所调查家庭6月份用水量的众数为吨，中位数为吨；

(3)、若该小区有300户居民，请根据抽样调查的样本平均数估计出这个小区6月份的用水量是多少吨？

查看试题解析
20. 已知一次函数 $y = - x + b$ 的图象与直线 $y = 3 x$ 相交于点 $P (m ， 3)$ ．

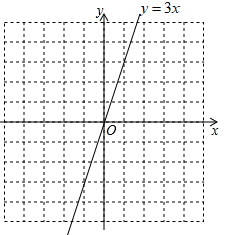(1)、求出b的值，并画出一次函数 $y = - x + b$ 的图象；

(2)、利用函数图象回答：不等式 $- x + b \leq 3 x$ 的解集为．

查看试题解析
21. 有一网络平台为7月份某品牌荔枝的销售设计了如下两种方案：
A方案：购买量不超过2千克时按标价销售，超过2千克时超过的部分按标价打折销售；
B方案：一律按标价的七折销售．
设销售量为x千克 $(x \geq 0)$ 时，A方案需要支付的费用为 $y_{1}$ 元，B方案需要支付的费用为 $y_{2}$ 元．

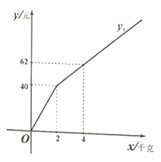(1)、该网络平台上这种品牌荔枝的标价为元/千克；

(2)、A方案需要支付的费用 $y_{1}$ 关于x的函数图象如图所示，求 $y_{1}$ 关于x的函数表达式；

(3)、当购买量在什么范围内时，选择A方案更优惠，请说明理由．

查看试题解析
22. 直线y=−2x+4与x轴，y轴分别交于A、B，过点A作AC⊥AB于点A，且AC=AB，点C在第一象限内．

(1)、求点A、B、C的坐标；

(2)、在第一象限内有一点P(3，t)，使S△PAB=S△ABC，求t的值．

查看试题解析
23. 已知矩形ABCD，AC、BD交于点O，过点O作 $E F ⊥ B D$ 分别交AB、CD于E、F．

(1)、求证：四边形BEDF是菱形．

(2)、若 $B C = 3$ ， $C D = 5$ ，求 $S_{菱形 B E D F}$ ．

查看试题解析
24. 当m，n为实数，且满足 $m + n m = n$ 时，就称点 $P (m ， \frac{m}{n})$ 为“状元点”．已知点A（0，7）和点M都在直线 $y = x + b$ 上，点B，C是“状元点”，且B在直线AM上．

(1)、求b的值及判断点F（2，6）是否为“状元点”；

(2)、请求出点B的坐标；

(3)、若 $A C \leq 5 \sqrt{2}$ ，求点C的横坐标的取值范围．

查看试题解析
25. 如图1，四边形ABCD是正方形，点E在正方形外角的平分线上，连接AE，记AE与对角线BD的交点为M．

(1)、求证： $A M = E M$ ；

(2)、如图2，点N是边AB的中点，连接MN，若 $M N = \sqrt{2} A N$ ，请探索BE与BD的数量关系，并说明理由；

(3)、在（2）的条件下，记BE与边CD的交点为点F，在BC边上取点P，使 $B P + D E = P F$ ，连接AP，AF，求 $∠ P A F$ 的度数．

查看试题解析

统计量	甲	乙	丙	丁
平均数	$9.2$	$9.2$	$9.2$	$9.2$
方差	$0.60$	$0.62$	$0.50$	$0.44$