安徽省芜湖市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 如果代数式 $\sqrt{2 - x}$ 在实数范围内有意义，那么x的取值范围是（）

A、 $x ⩽ 2$ B、 $x ⩾ 2$ C、 $x ⩽ - 2$ D、 $x ⩾ - 2$

查看试题解析
2. 下列二次根式中，不能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{18}$ D、 $\sqrt{12}$

查看试题解析
3. 一次函数 $y = (m - 3) x + m + 6$ 中，y随x的增大而减小，则m的取值范围是（）

A、 $m > 3$ B、 $m < 3$ C、 $m ⩾ 3$ D、 $m ⩽ 3$

查看试题解析
4. 实数 $a ， b$ 在数轴上的位置如图所示，则化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、 $- 2 b$ B、 $- 2 a$ C、 $2 (b - a)$ D、0

查看试题解析
5. 如图，在▱ABCD中，BC=10，AC=8，BD=14，则△AOD的周长是（）

A、32 B、23 C、21 D、20

查看试题解析
6. 一次函数 $y = - x - 1$ 不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为（）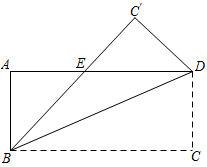

A、3 B、4 C、5 D、6

查看试题解析
8. 新冠肺炎疫情期间，某市实施静态管理，九年级某班组建了若干个数学学习互助小组，其中一个9人小组进行数学线上学习效果的自测，九名学生的平均成绩为73分，若将他们的成绩从高分到低分排序后，前五名学生的平均成绩为85分，后五名学生的平均成绩为63分，则这九名学生成绩的中位数是（）

A、84 B、83 C、74 D、73

查看试题解析
9. 一个样本为1，3，2，2，a，b，c，已知这个样本的众数为 $3$ ，平均数为2，那么这个样本的方差为（）

A、 $\frac{3}{7}$ B、 $\frac{4}{7}$ C、 $\frac{5}{7}$ D、 $\frac{8}{7}$

查看试题解析
10. 如图，△ABC的面积是24，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（）

A、9 B、10 C、11 D、12

查看试题解析
11. 如图，菱形ABCD中，AC＝48，BD＝14，DH⊥AB于点H，则线段BH的长为（）

A、 $\frac{48}{25}$ B、 $\frac{98}{25}$ C、 $\frac{168}{25}$ D、 $\frac{336}{25}$

查看试题解析
12. 在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，如图，折线段表示甲、乙两车之间的距离y（千米）与行驶时间x（小时）的函数关系的图象，下列说法错误的是（）

A、乙先出发的时间为0.5小时 B、甲的速度比乙的速度快 C、甲出发0.4小时后两车相遇 D、甲到B地比乙到A地迟5分钟

查看试题解析

二、填空题

13. 海伦一秦九韶公式告诉我们：三角形的三边长分别为a，b，c，记 $p = \frac{1}{2} (a + b + c)$ ，那么三角形面积可以表示为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．现已知一个三角形的三边长分别为5、6、7，那么这个三角形的面积为．

查看试题解析
14. 若 $y + 3 = \frac{\sqrt{x - 2} + \sqrt{2 - x}}{4}$ ，则 $x^{y}$ ＝．

查看试题解析
15. 一次函数y= -2x+4的图象与坐标轴所围成的三角形面积是 .

查看试题解析
16. 如图，正方形ABCD的边长为4，点E是AD的中点，沿BE所在直线折叠△ABE，得到△FBE，延长BF交CD于G点，则DG的长为．

查看试题解析
17. 如图，正比例函数 $y = m x$ 与一次函数 $y = a x + b$ 相交于点P，则关于x的不等式组 ${\begin{array}{l} m x > 0 \\ a x + b < 0 \end{array}$ 的解集为．

查看试题解析
18. 如图，正方形ABCD的边长为8，点E在AB上，BE＝2，点M，N为AC上动点，且 $M N = 2 \sqrt{2}$ ，连接BN，EM，则四边形BEMN周长的最小值为．

查看试题解析

三、解答题

19. 计算： $\frac{1}{\sqrt{3} + 1} - (\sqrt{3} - 2) (1 - \sqrt{3})$ ．

查看试题解析
20. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

(1)、试判断△ABC的形状，并说明理由；

(2)、在格点上找一点D，使四边形ABCD是平行四边形，请画出这个四边形ABCD．

查看试题解析
21. 某市运行了一种新型公共交通班车，下表是某一天对该班车载客量的统计，请根据所学知识计算这天平均每班车的载客量是多少？（结果取整数）
载客量/人
频数（班次）
$1 \leq x < 21$
3
$21 \leq x < 41$
5
$41 \leq x < 61$
20
$61 \leq x < 81$
22
$81 \leq x < 101$
18
$101 \leq x < 121$
17

查看试题解析
22. 如图，直线y=kx-6经过点A（4，0），直线y=-3x+3与x轴交于点B，且两直线交于点C．

(1)、求k的值；

(2)、求△ABC的面积.

查看试题解析
23. 如图，△ABC中， $M N ∥ B D$ 交AC于P，∠ACB，∠ACD的平分线分别交MN于E、F．

(1)、求证： $P E = P F$ ；

(2)、当MN与AC的交点P在AC的什么位置时，四边形AECF是矩形，说明理由；

(3)、当△ABC满足什么条件时，四边形AECF是正方形．（不需要证明）

查看试题解析

载客量/人	频数（班次）
$1 \leq x < 21$	3
$21 \leq x < 41$	5
$41 \leq x < 61$	20
$61 \leq x < 81$	22
$81 \leq x < 101$	18
$101 \leq x < 121$	17