安徽省淮北市五校联考2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式是最简二次根式的为（）

A、 $\sqrt{10}$ B、 $\sqrt{20}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{3.6}$

查看试题解析
2. 下列数据能作为直角三角形三边长的是（）

A、6，7，8 B、1， $\sqrt{3}$ ， 2 C、5，12，14 D、7，24，26

查看试题解析
3. 如果对甲、乙两种产品进行对比实验，得知乙产品性能比甲产品性能更稳定，那么分析计算它们的方差 $S_{甲}^{2}$ 、 $S_{乙}^{2}$ 的大小关系是（）

A、 $S_{甲}^{2} > S_{乙}^{2}$ B、 $S_{甲}^{2} < S_{乙}^{2}$ C、 $S_{甲}^{2} = S_{乙}^{2}$ D、都不对

查看试题解析
4. 一元二次方程 $x^{2} - 4 x - 5 = 0$ 经过配方后，可变形为（）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x + 2)}^{2} = - 1$ C、 ${(x - 2)}^{2} = 9$ D、 ${(x + 2)}^{2} = 9$

查看试题解析
5. 甲乙两台机床同时生产同一种零件，在某周的工作日内，两台机床每天生产次品的个数整理成甲、乙两组数据，如下表：关于以上数据，下列说法正确的是（）
机床/星期
星期一
星期二
星期三
星期四
星期五
甲
2
0
4
3
2
乙
1
3
4
0
4

A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数大于乙的平均数 D、甲的方差小于乙的方差

查看试题解析
6. 如图，平行四边形ABCD中，两对角线交于点O，AB⊥AC，AD=5cm，OC=2cm，则对角线BD的长为（）

A、 $\sqrt{13}$ cm B、8cm C、3cm D、 $2 \sqrt{13}$ cm

查看试题解析
7. 《九章算术》勾股章有一问题，其意思是：现有一竖立着的木柱，在木柱上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺，牵着绳索退行，在离木柱根部8尺处时绳索用尽，请问绳索有多长？若设绳索长度为x尺，根据题意，可列方程为（）

A、 $8^{2} ﹢ x^{2} = {(x ﹣ 3)}^{2}$ B、 $8^{2} ﹢ {(x + 3)}^{2} = x^{2}$ C、 $8^{2} ﹢ {(x ﹣ 3)}^{2} = x^{2}$ D、 $x^{2} ﹢ {(x ﹣ 3)}^{2} = 8^{2}$

查看试题解析
8. 若菱形ABCD中，AE垂直平分BC于E，AE=1cm，则BC的长是（）

A、1cm B、 $\frac{2 \sqrt{3}}{3}$ cm C、3cm D、4cm

查看试题解析
9. 若实数a，b，c满足 $a + b + c = 0$ ，则（）

A、 $b^{2} - 4 a c > 0$ B、 $b^{2} - 4 a c < 0$ C、 $b^{2} - 4 a c \geq 0$ D、 $b^{2} - 4 a c \leq 0$

查看试题解析
10. 如图．在△ABC中，∠ACB＝60°，AC＝1，D是边AB的中点，E是边BC上一点．若DE平分△ABC的周长，则DE的长为（　　）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{5}{3}$

查看试题解析

二、填空题

11. 关于 $x$ 的一元二次方程 $x^{2} + x - a = 0$ 的一个根是2，则另一个根是．

查看试题解析
12. 若一个多边形的外角和是内角和的 $\frac{1}{3}$ ，则这个多边形的边数是.

查看试题解析
13. 如图，在△ABC中，∠BAC=90°，AD是BC边上的高，E、F分别是AB、AC边的中点，若AB=8，AC=6，则△DEF的周长为．

查看试题解析
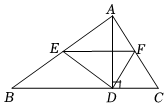14. 如图，已知矩形 $A B C D$ ， $A B = 8$ ， $A D = 4$ ， E为CD边上一点， $C E = 5$ ，点P从点B出发，以每秒1个单位长度的速度沿着BA边向终点A运动，连接PE，设点P运动的时间为t秒，请探究下列问题．

(1)、 $A E =$ ；

(2)、当 $t =$ 时， $△ P A E$ 是以PE为腰的等腰三角形．

查看试题解析

三、解答题

15. 计算： $\sqrt{\frac{1}{3}} + \sqrt{6} \times (\frac{1}{\sqrt{2}} + \sqrt{8}) - | \sqrt{3} - 2 |$ ．

查看试题解析
16. 解方程： $x^{2} - 1 = 3 (x + 1)$

查看试题解析
17. .已知如图，DC＝4，AC＝3，∠ACD＝90°，AB＝13，BD＝12.
试求出：

(1)、∠ADB的度数.

(2)、求出△ABD的面积.

查看试题解析
18. 图1，图2均为4×4的正方形网格，每个小正方形的顶点被称为格点，小正方形的边长都为1，线段AB的端点均在格点上．按要求在图1，图2中画图．

(1)、在图1中，以线段AB为一边，画一个矩形，且使其面积为4，其余两个顶点均为格点；

(2)、在图2中，以线段AB为对角线，画一个面积是4的菱形，且其余两个顶点均为格点．

查看试题解析
19. 如图，在平行四边形ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF，AC，且AD＝AF．

(1)、判断四边形ABFC的形状并证明；

(2)、若AB＝3，∠ABC＝60°，求EF的长．

查看试题解析
20. 用一面足够长的墙为一边，其余各边用总长42米的围栏建成如图所示的生态园，中间用围栏隔开．由于场地限制，垂直于墙的一边长不超过7米．（围栏宽忽略不计）

(1)、若生态园的面积为144平方米，求生态园垂直于墙的边长；

(2)、生态园的面积能否达到150平方米？请说明理由．

查看试题解析
21. 如图，在 $△ A B C$ 中，点D，E分别为BC，AC边上的中点，BE＝2DE，过点A作 $A F ∥ B E$ 交DE延长线于点F．

(1)、求证：四边形ABEF为菱形；

(2)、若∠ABE＝ $45 °$ ， AB＝4，求四边形ABDF的面积．

查看试题解析
22. 为了了解全区八年级学生学业考试体育成绩，现从中随机抽取n名学生的体育成绩进行分段（A：30分；B：29~25分；C：24~20分；D：19~10分；E：9~0分），统计图和统计表如下所示．
学生考试体育成绩（分数段）统计表
分数段
频数（人）
百分比
A
48
a
B
b
25%
C
84
35%
D
36
c
E
12
5%
根据上面提供的信息，回答下列问题，

(1)、n＝， a＝， b＝；

(2)、补全统计图；

(3)、若绘制“学生学业考试体育成绩扇形统计图”，则体育成绩在A段所对应扇形的圆心角度是．

(4)、如果将成绩在25分以上（含25分）定为优秀，那么该区今年8000名八年级学生中体育成绩为优秀的学生约有多少名？

查看试题解析
23. 如图，在正方形ABCD中，点E在边CD上，连接AE，过点A作 $A F ⊥ A E$ 交CB的延长线于点F，连接EF，AG平分∠FAE，AG分别交BC，EF于点G，H，连接EG，DH．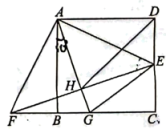

(1)、求证：AF＝AE；

(2)、若∠BAG＝10°，求∠EGC的度数；

(3)、若DE＝CE，求CE：CG：EG的值．

查看试题解析

机床/星期	星期一	星期二	星期三	星期四	星期五
甲	2	0	4	3	2
乙	1	3	4	0	4

分数段	频数（人）	百分比
A	48	a
B	b	25%
C	84	35%
D	36	c
E	12	5%