陕西省咸阳市武功县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期：2022-07-22 类型：期末考试
一、选择题。（共8小题，每小题3分，计24分。每小题只有一个选项是符合题意的）
-
1. 下面图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 华为作为世界顶级科技公司，设计的麒麟90005GSoC芯片，拥有领先的5nm制程和架构设计，5nm＝0.000000005m，将0.000000005用科学记数法表示为（ ）A、5×10﹣7 B、5×10﹣8 C、5×10﹣9 D、5×10﹣103. 下列事件中，是必然事件的是（ ）A、明天气温会下降 B、下午考试，小明会考满分 C、乘坐公共汽车恰好有空座 D、三角形的内角和是180°4. 以下列各组线段为边，能组成三角形的是（ ）A、2、2、4 B、8、6、3 C、2、6、3 D、11、4、65. 下列运算正确的是（ ）A、7a3﹣3a2＝4a B、（a2）3＝a5 C、a6÷a3＝a2 D、﹣a（﹣a+1）＝a2﹣a6. 如图，给出下列条件：①∠1＝∠3；②∠3＝∠5；③∠4+∠7＝180°；④∠5+∠3＝180°．
能判断a∥b的是（ ）
A、①②④ B、①③④ C、①②③④ D、①②7. 如图，在水平地面上的甲、乙两个区域分别由若干个大小完全相同的正三角形瓷砖组成，小红在甲、乙两个区域内分别随意抛一个小球，P（甲）表示小球停留在甲区域中黑色部分的概率，P（乙）表示小球停留在乙区域中黑色部分的概率，下列说法中正确的是（ ）
A、P（甲）＝P（乙） B、P（甲）＞P（乙） C、P（甲）＜P（乙） D、P（甲）与P（乙）的大小无法确定8. 下表反映的是某地区电的使用量x（千瓦•时）与应交电费y（元）之间的关系，下列说法不正确的是（ ）用电量x（千瓦•时）
1
2
3
4
…
应交电费y（元）
0.55
1.1
1.65
2.2
…
A、x与y都是变量，且x是自变量，y是因变量 B、用电量每增加1千瓦•时，电费增加0.55元 C、若用电量为8千瓦•时，则应交电费4.4元 D、若所交电费为2.75元，则用电量为6千瓦•时二、填空题。（共5小题，每小题3分，共15分）
-
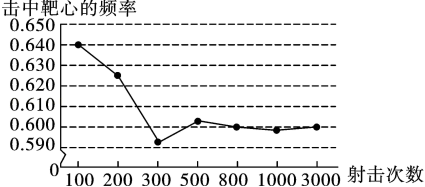
9. 用平方差公式计算：799×801﹣8002＝ ．10. 如图，是某射手在相同条件下进行射击训练的结果统计图，则该射手击中靶心的概率估计值为 ． （结果精确到0.1）
11. 如图，在△ABC中，∠C＝90°，AD是△ABC的角平分线．DE⊥AB于点E，若CD＝4cm，则DE的长为cm．
12. 如图，E是△ABC的边AC的中点，过点C作CF∥AB，过点E作直线DF交AB于D，交CF于F，若AB＝9，CF＝6.5，则BD的长为 ．
13. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，在AD上取一点E，连接CE，使得AE＝CE，若∠ECD＝20°，则∠B＝ ．
三、解答题。（共13小题，计81分.解答应写出过程）
-
14. 计算：（﹣1）2020+（﹣3.14）0+（﹣ ）﹣2 ．15. 如图，在边长为1的正方形网格中，△ABC的三个顶点都在格点上，在图中画出△ABC关于直线l对称的△A'B'C'．
16. 先化简，再求值：[（x﹣2y）2+（x﹣2y）（x+2y）]÷x，其中x＝2，y＝﹣1．17. 如图，已知△ABC，利用尺规作∠BAC的角平分线AD，交BC于点D．（保留作图痕迹，不写作法）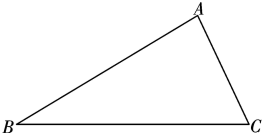
18. 如图所示，在△ABC中，∠BAC＝105°，若MP和NQ分别垂直平分AB和AC．求∠PAQ的度数．
19. 小明家距离学校8千米．一天早晨，小明骑车上学途中自行车出现故障，他于原地修车，车修好后，立即在确保安全的前提下以更快的速度匀速骑行到达学校．如图反映的是小明上学过程中骑行的路程（千米）与他所用的时间（分钟）之间的关系，请根据图象，解答下列问题：
(1)、小明骑行了千米时，自行车出现故障；修车用了分钟；(2)、求自行车出现故障前小明骑行的平均速度．20. 如图，在四边形ABCD中，E是对角线AC上一点，连接DE，AD∥BC，AC＝AD，∠CED+∠B＝180°．△ADE与△CAB全等吗？为什么？
21. 华氏温度f（℉）与摄氏温度c（℃）之间存在如下的关系f＝ c+32．(1)、一个人的体温有可能达到100℉吗（精确到0.1）？(2)、如果某地早晨的摄氏温度为15℃，那么此地早晨的华氏温度是多少？(3)、若当地某一时刻的华氏温度为68℉，则该时刻摄氏温度是多少？22. 如图，小明和小华住在同一个小区不同单元楼，他们想要测量小明家所在单元楼AB的高度，首先他们在两栋单元楼之间选定一点E，然后小华在自己家阳台C处测得E处的俯角为∠1，小明站在E处测得楼顶A的仰角为∠2，发现∠1与∠2互余，过点F作FG⊥AB于点G，已知BG＝1米，BE＝CD＝20米，BD＝58米，点B、E、D在一条直线上，AB⊥BD，FE⊥BD，CD⊥BD，试求单元楼AB的高．（注：BE＝FG，BG＝EF，∠1与∠3互余）
23. 如图，某市有一块长方形地块用来建造住宅、广场和商厦．住宅用地是长为（3a+2b）米，宽为4a米的长方形，广场是长为3a米，宽为（2a﹣b）米的长方形．
(1)、这块用地的总面积是多少平方米？(2)、求出当a＝30，b＝50时商厦的用地面积．24. 有7张纸签，分别标有数字1，2，3，4，5，6，7，小明先从中任意抽取一张纸签（不放回），小颖再从剩余的纸签中任意抽取一张，谁抽到的数字大谁就获胜，然后两人把抽到的纸签都放回，重新开始游戏．(1)、现小明已经抽到数字4，然后小颖抽纸签，那么小明获胜的概率是多少？小颖获胜的概率又是多少？(2)、若小明已经抽到数字6，小明、小颖获胜的概率分别是多少？若小明已经抽到数字1，情况又如何？25. 如图，已知直线AB，CD，AC上的点M，N，E满足ME⊥NE，∠AME+∠CNE＝90°，∠ACD的平分线CG交MN于G，作射线GF∥AB．
(1)、直线AB与CD平行吗？为什么？(2)、若∠CAB＝66°，求∠CGF的度数．26. 如图，CD是经过∠BCA顶点C的一条直线，CA＝CB，E，F分别是直线CD上的两点，且∠BEC＝∠CFA＝α．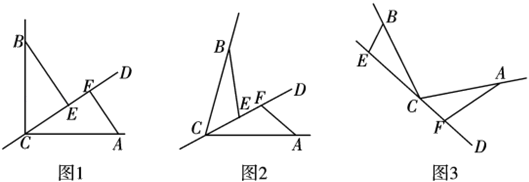
(1)、若直线CD经过∠BCA的内部，且点E，F在射线CD上（点E靠近点C）；①如图1，若∠BCA＝90°，α＝90°，则BE CF；（填“＞”“＜”或“＝”）
②如图2，若0°＜∠BCA＜90°，请添加一个关于α与∠BCA数量关系的条件，使①中的结论仍然成立，并说明理由．
(2)、如图3，若直线CD经过∠BCA的外部，α＝∠BCA，请提出关于EF，BE，AF这三条线段的数量关系的合理猜想，并说明理由．