四川省广安市邻水县2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-07-22 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。）

1. 函数 $y = \sqrt{4 - 2 x}$ 中，自变量x的取值范围是（）

A、x≤2 B、x＜2 C、x≥2 D、x＞2

查看试题解析
2. 下列各式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{20}$

查看试题解析
3. 一个直角三角形的两条边的长分别为8，10，则第三条边的长为（）

A、6 B、12 C、 $2 \sqrt{41}$ D、6或 $2 \sqrt{41}$

查看试题解析
4. 如图，菱形ABCD的对角线AC，BD相交于点O，E为AB的中点，连接OE．若菱形ABCD的周长为32，则OE的长为（）

A、16 B、12 C、8 D、4

查看试题解析
5. 某校举办了以“展礼仪风采，树文明形象”为主题的比赛．已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为95分、92分、80分．若依次按照40%，25%，35%的百分比确定成绩，则该选手的最终成绩是（）

A、88分 B、89分 C、90分 D、91分

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $3 \sqrt{5} - \sqrt{5} = 3$ C、 $\sqrt{\frac{1}{3}} \times \sqrt{27} = 3$ D、 $\sqrt{6} \div \sqrt{3} = 2$

查看试题解析
7. 在△ABC中，BC²﹣AC²＝AB².若∠B＝25°，则∠C＝（）

A、20° B、35° C、65° D、75°

查看试题解析
8. 下列关于一次函数y＝﹣x+1的说法中，错误的是（）

A、其图象经过第一、二、四象限 B、其图象与x轴的交点坐标为（﹣1，0） C、当x＞0时，y＜1 D、y随x的增大而减小

查看试题解析
9. 如图，在矩形ABCD中，对角线AC，BD相交于点E，BF∥AC，CF∥BD．若四边形BECF的面积为2，则矩形ABCD的面积为（）

A、4 B、6 C、8 D、16

查看试题解析
10. 清明假期第一天天气晴朗，小明和爸爸去爬山．小明和爸爸同时从山脚出发，由于爸爸有爬山经验，匀速爬到山顶．小明刚开始的速度比爸爸快，累了之后减速继续爬山，和爸爸相遇后0.5h才加速追赶爸爸，最终爸爸用2h爬到了山顶，小明比爸爸晚了6min到达．他们出发的时间x（单位：h）与爬山的路程y（单位：km）的函数图象如图所示，则下列说法错误的是（）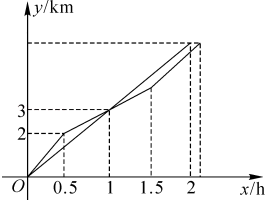

A、爸爸爬山的速度为3km/h B、1.5h时爸爸与小明的距离为0.5km C、山脚到山顶的总路程为6km D、小明加速追赶爸爸时的速度为3km/h

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分．请将最简答案填写在答题卡相应位置）

11. 化简： $\sqrt{{(- \frac{1}{2})}^{2}}$ ＝．

查看试题解析
12. 疫情期间居家学习，双胞胎姐妹小兰和小丽积极进行体育锻炼，增强体质．她们进行1分钟跳绳比赛，每人5次跳绳成绩的平均数都是105个，方差分别是s_小兰²＝1.6，s_小丽²＝2.2，则这5次跳绳成绩更稳定的是．（填“小兰”或“小丽”）

查看试题解析
13. 将直线y＝2x﹣1向上平移4个单位长度，平移后直线的函数解析式为．

查看试题解析
14. 如图，在▱ABCD中，∠D+∠B＝220°，AE平分∠DAB交CD于点E，则∠DEA的度数为．

查看试题解析
15. 如图，一棵9m高的树被风刮断了，树顶落在离树根6m处，则折断处的高度AB为m．

查看试题解析
16. 如图，正方形ABCD和正方形EFCG的边长分别为3，1，点F，G分别在边BC，CD上，P为AE的中点，连接PG，则PG的长为．

查看试题解析

三、解答题（本大题共4小题。第17小题5分，第18、19、20小题各6分，共23分）

17. 计算： $2 \sqrt{2} - \sqrt{24} \div \sqrt{3} + {(\sqrt{2} - 1)}^{2}$ ．

查看试题解析
18. 如图，已知AD是Rt△ABC的斜边BC上的中线，分别过点A，B作BC，AD的平行线，两直线交于点E．求证：四边形ADBE是菱形．

查看试题解析
19. 如图，4×4方格纸上每个小正方形的边长都为1．

⑴在方格纸上画一个面积为8的正方形（四个顶点都在格点上）；

⑵用圆规在数轴上找出表示 $\sqrt{8}$ 的点（保留作图痕迹）．

查看试题解析
20. 如图，在平面直角坐标系中，过点A（﹣6，0）的直线l₁：y₁＝kx+b与直线l₂：y₂＝2x相交于点B（m，4）．

(1)、求直线l₁的函数解析式；

(2)、利用函数图象直接写出当y₂≤y₁时，x的取值范围为．

查看试题解析

四、实践应用题（本大题共4小题。第21小题6分，第22、23、24小题各8分，共30分）

21. 某中学在校园一角开辟了一块四边形的试验田，把课堂的“死教材”转换为生动的“活景观”，学生们在课堂上学习理论之余，还可以到试验田实际操练．如图，四边形ABCD是规划好的试验田，经过测量得知：∠ADC＝90°，CD＝3m，AD＝4m，AB＝13m，BC＝12m．求试验田ABCD的面积．

查看试题解析
22. 在解决问题“已知a＝ $\frac{1}{\sqrt{2} - 1}$ ，求3a²﹣6a﹣1的值”时，小明是这样解答的：
∵a＝ $\frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} + 1$ ，

∴a﹣1＝ $\sqrt{2}$ ，

∴（a﹣1）²＝2，即a²﹣2a+1＝2，

∴a²﹣2a＝1，

∴3a²﹣6a＝3，

∴3a²﹣6a﹣1＝2．

请你根据小明的解答过程，解决下面的问题：

若a＝ $\frac{2}{3 - \sqrt{7}}$ ，求2a²﹣12a+1的值．

查看试题解析
23. 在学校举办的“读书月”活动中，八（3）班的李梅调查了班级里所有同学本学期购买课外书的费用情况，并将结果绘制成如图所示的统计图．

请根据以上信息，解答下列问题：

(1)、八（3）班同学购买课外书费用的众数为元，中位数为元；

(2)、求八（3）班同学购买课外书费用的平均数；

(3)、若该校八年级共有学生200人，根据调查数据，估计该校八年级学生本学期购买课外书共花费了的钱数．

查看试题解析
24. 为了更好地运用信息技术辅助教学，某校计划购买A，B两种型号的笔记本电脑共11台．已知A型笔记本电脑每台4500元，B型笔记本电脑每台5500元．设购买A型笔记本电脑x台，购买两种型号笔记本电脑的总费用为y元．

(1)、求y关于x的函数关系式；

(2)、若购买B型笔记本电脑的数量多于A型笔记本电脑的数量，请给出一种总费用最低的方案，并求出该方案所需的总费用．

查看试题解析

五、推理论证题

25. 如图，在▱ABCD中，AC⊥AD，作∠ECA＝∠ACD，CE交AB于点O，交DA的延长线于点E，连接BE．

(1)、求证：四边形ACBE是矩形；

(2)、连接OD，若AB＝4，∠ACD＝60°，求OD的长．

查看试题解析

六、拓展探索题

26. 如图1，BD是边长为1的正方形ABCD的对角线，BE平分∠DBC交DC于点E，延长BC到点F，使CF＝CE，连接DF，交BE的延长线于点G．

(1)、求证：△BCE≌△DCF；

(2)、求CF的长；

(3)、在AB上取一点H，使BH＝CF，以BC所在直线为x轴，AB所在直线为y轴建立如图2所示的平面直角坐标系，在直线BD上是否存在点P，使得以B，H，P为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析