2021-2022学年苏科版数学八年级上册1.3.3探索三角形全等的条件AAS同步训练

试卷更新日期：2022-07-22 类型：同步测试

进入出卷网下载

一、单选题

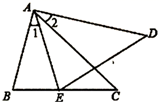
1. 如图，AC=DF，∠1=∠2，如果根据“AAS”判定△ABC≌△DEF，那么需要补充的条件是（）

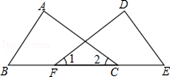A、∠A=∠D B、AB=DE C、BF=CE D、∠B=∠E

查看试题解析
2. 如图， $D$ 、 $E$ 分别为 $A B$ 、 $A C$ 边上的点， $∠ B = ∠ C$ ， $B E = C D$ .若 $A B = 7$ ， $C E = 4$ ，则 $A D$ 的长度为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 如图， $Δ A B C$ 和 $Δ D F E$ 中，点 $B$ ， $E$ ， $C$ ， $F$ 在同一直线上，在① $A B = D F$ ，② $B E = F C$ ，③ $∠ A C B = ∠ D E F$ ，④ $∠ A = ∠ D$ ，⑤ $∠ B = ∠ F$ 五个条件中，能使 $Δ A B C$ 与 $Δ D F E$ 全等的条件的序号是（）

A、①②③ B、①②④ C、①③④ D、③④⑤

查看试题解析
4. 如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD是等腰三角形，EB=ED；②折叠后∠ABE和∠CBD一定相等；③△EBA和△EDC一定是全等三角形.其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 如图，点B，C，E在同一直线上，且 $A C = C E$ ， $∠ B = ∠ D = 90 °$ ， $A C ⊥ C D$ ，下列结论不一定成立的是（）

A、 $∠ A = ∠ 2$ B、 $∠ A + ∠ E = 90 °$ C、 $B C = D E$ D、 $∠ B C D = ∠ A C E$

查看试题解析
6. 如图， $∠ A C B = 90 °$ ，AC=BC. $A D ⊥ C E$ ， $B E ⊥ C E$ ，垂足分别是点D、E.若AD=6，BE=2，则DE的长是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

7. 如图， $△ A B C$ 与 $△ D C B$ 中，已知， $∠ A = ∠ D$ ，请你添加一个条件（不添加字母和辅助线），使 $△ A B C ≌ △ D C B$ ，你添加的条件是.

查看试题解析
8. 如图， $A C = D E$ ， $∠ 1 = ∠ 2$ ，要使 $△ A B C ≌ △ D B E$ 还需添加一个条件是．（只需写出一种情况）

查看试题解析
9. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC＝BC，∠ACB＝90°)，点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm.

查看试题解析
10. 如图，点 $A$ ， $C$ 在直线 $l$ 上， $A E ⊥ A B$ 且 $A E = A B$ ， $B C ⊥ C D$ 且 $B C = C D$ ，过 $E$ ， $B$ ， $D$ 分别作 $E F ⊥ l$ ， $B G ⊥ l$ ， $D H ⊥ l$ ，若 $E F = 6$ ， $B G = 3$ ， $D H = 4$ ，则 $△ A B C$ 的面积是．

查看试题解析
11. 如图所示，∠E＝∠F＝90°，∠B＝∠C ， AE＝AF ．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN ．其中正确的结论是．（将你认为正确的结论的序号都填上）

查看试题解析
12. 如图，在△ABC中，点D为BC的中点，△AEF的边EF过点C，且AE=EF，AB∥EF，AD平分∠BAE，CE=2，AB=9，则CF= ．

查看试题解析

三、解答题

13. 如图，点E、F在AB上，且AE＝BF，∠C＝∠D，AC∥BD.求证：CF∥DE.

查看试题解析
14. 如图，△ABC与△BAD中，AD与BC相交于点M ， ∠1＝∠2， ▲ ，试说明△ABC≌△BAD ．请你在横线上添加一个条件，使得它可以用“AAS”来说明△ABC≌△BAD ，并写出说理过程．

查看试题解析
15. 如图， $A B = A E$ ， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ， $∠ B = 60 °$ ．

(1)、试说明： $△ A B C ≌ △ A E D$ ；

(2)、求 $∠ A E D$ 的度数．

查看试题解析
16. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，直线 $M N$ 经过点 $C$ ，且 $A D ⊥ M N$ 于 $D$ ， $B E ⊥ M N$ 于 $E$ .

(1)、当直线 $M N$ 绕点 $C$ 旋转到图1的位置时，

①求证： $△ A D C$ ≌ $△ C E B$ ；

②求证： $D E = A D + B E$ ；

(2)、当直线 $M N$ 绕点 $C$ 旋转到图2的位置时，（1）中的结论②还成立吗？若成立，请给出证明；若不成立，说明理由.

查看试题解析