（人教版）2022-2023学年度第一学期九年级数学24.1.2 垂直于弦的直径 同步测试
试卷更新日期：2022-07-21 类型：同步测试
一、单选题
-
1. 如图，在⊙O中，CD是⊙O的直径，AB⊥CD于点E，若AB＝8，CE＝2，则⊙O的半径为（ ）
A、 B、 C、3 D、52. 如图，⊙O的半径为5，弦AB＝6，P是弦AB上的一个动点（不与A、B重合），下列符合条件的OP的值可以是（ ）
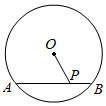A、3.1 B、4.2 C、5.3 D、6.43. 如图，在⊙O中，OC⊥AB，若∠BOC＝40°，则∠OAB等于（ ）
A、40° B、50° C、80° D、120°4. 如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB＝8，OC＝3，则EC的长为（ ）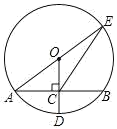
A、2 B、8 C、2 D、25. 在圆柱形油槽内装有一些油，截面如图所示，已知截面⊙O半径为5cm，油面宽AB为6cm，如果再注入一些油后，油面宽变为8cm，则油面AB上升了（ ）cm
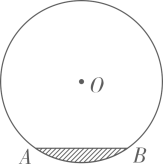A、1 B、3 C、3或4 D、1或76. 往直径为78cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽 ， 则水的最大深度为（ ）
A、36 cm B、27 cm C、24 cm D、15 cm7. 半径等于4的圆中，垂直平分半径的弦长为（ ）A、 B、 C、 D、8. 如图，的直径 ， CD是的弦， ， 垂足为P，且 ， 则CD的长为（ ）．
A、3 B、4 C、 D、9. 如图，AB是⊙O的直径，⊙O的弦CD＝8，且CD⊥AB于点E．若OE∶OB＝3∶5，则直径AB的长为（ ）
A、5 B、10 C、12 D、10. 如图，△ABC中，AB＝AC＝4 ， BC＝8，则△ABC外接圆的直径为（ ）
A、8 B、10 C、12 D、16二、填空题
-
11. 如图，CD是⊙O的直径，AB是弦，CD⊥AB，若OB＝5，AB＝8，则AC的长为 ．
12. 数学活动课上，小东想测算一个圆形齿轮内圈圆的半径．如图所示，小东首先在内圈圆上取点A，B，再作弦AB的垂直平分线，垂足为C，交于点D，连接CD，经测量cm，cm，那么这个齿轮内圈圆的半径为cm．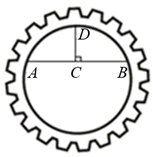
13. 如图，舞台地面上有一段以点O为圆心的 ， 某同学要站在的中点C的位置上．于是他想：只要从点O出发，沿着与弦垂直的方向走到上，就能找到的中点C，老师肯定了他的想法．这位同学确定点C所用方法的依据是 ．
14. 如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB=10，CD=8，则OH的长为
15. 为了落实“双减”政策，朝阳区一些学校在课后服务时段开设了与冬奥会项目冰壶有关的选修课．如图，在冰壶比赛场地的一端画有一些同心圆作为营垒，其中有两个圆的半径分别约为60cm和180 cm，小明掷出一球恰好沿着小圆的切线滑行出界，则该球在大圆内滑行的路径MN的长度为cm．
三、解答题
-
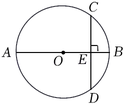
16. 如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB＝10，BE＝2，求弦CD的长．
17. 如图，是的弦，C是上的一点，且 ， 于点E，交于点D．若的半径为6，求弦的长．
18. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC＝10cm，CD＝16cm，求AE的长．
19. 如图，AB是⊙O的弦，C、D为直线AB上两点，OC＝OD，求证：AC＝BD.
20. 如图，有一座圆弧形拱桥，它的跨度为 ， 拱高为 ， 当洪水泛滥到跨度只有时，就要采取紧急措施，若某次洪水中，拱顶离水面只有 ， 即时，试通过计算说明是否需要采取紧急措施.
21. 如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切于点C时，另一边与圆两个交点A和B的读数恰好为“2”和“8”（单位：cm）求该圆的半径．
