福建省宁德市2021-2022学年高一上学期数学期末质量检测试卷
试卷更新日期:2022-07-21 类型:期末考试
一、单选题
-
1. 已知集合A={1,2,3},B={x∈N|x≤2},则A∪B=( )A、{2,3} B、{0,1,2,3} C、{1,2} D、{1,2,3}2. 命题“”的否定是( )A、 B、 C、 D、3. 已知弧长为的弧所对的圆心角为 , 则该弧所在的扇形面积为( )A、 B、 C、 D、4. 不等式恒成立,则的取值范围为( )A、 B、或 C、 D、5. 已知 , 则( )A、 B、 C、 D、6. 已知函数是定义在上的奇函数, , 且 , 则( )A、-1 B、0 C、1 D、27. 已知函数 , , 的零点分别为则的大小顺序为( )A、 B、 C、 D、8. 已知函数的图象的一部分如图1所示,则图2中的函数图象对应的函数解析式为( )
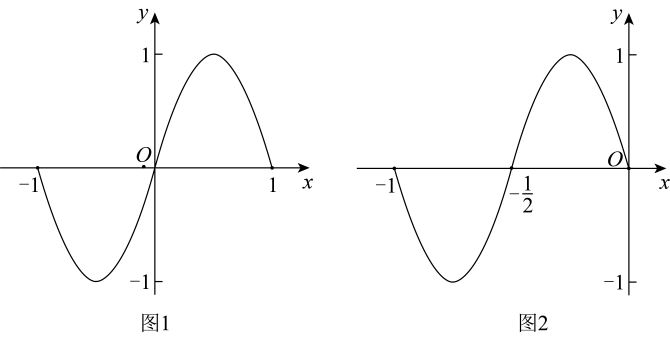 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列函数中,既是偶函数又在区间上是增函数的是( )A、 B、 C、 D、10. 若 , 则下列不等式正确的是( )A、 B、 C、 D、11. 若函数 , 则下列选项正确的是( )A、最小正周期是 B、图象关于点对称 C、在区间上单调递增 D、图象关于直线对称12. 设 , 用表示不超过x的最大整数,则称为高斯函数,也叫取整函数.令 , 以下结论正确的是( )A、 B、为偶函数 C、最小正周期为 D、的值域为
三、填空题
-
13. .14. 请写出一个同时满足下列两个条件的函数:.
(1) ,若则(2)15. 在平面直角坐标系中,以轴为始边作两个锐角 , , 它们的终边分别与单位圆相交于 , 两点, , 的纵坐标分别为 , . 则的终边与单位圆交点的纵坐标为.16. 已知函数 , 使方程有4个不同的解: , 则的取值范围是;的取值范围是.四、解答题
-
17. 设集合 , , .(1)、 , 求;(2)、若“”是“”的充分条件,求的取值范围.18. 已知是上的奇函数,且 .(1)、求的解析式;(2)、判断的单调性,并根据定义证明.19. 已知函数 , 只能同时满足下列三个条件中的两个:
①的解集为;
②;
③最小值为-4.
(1)、请写出这两个条件的序号,求的解析式;(2)、求关于的不等式的解集.20. 已知 .(1)、设 , 求的值域;(2)、设 , 求的值.21. 闽东传承着中国博大精深的茶文化,讲究茶叶茶水的口感,茶水的口感与茶叶类型和水的温度有关.如果刚泡好的茶水温度是 , 空气的温度是 , 那么分钟后茶水的温度(单位:)可由公式求得,其中是一个物体与空气的接触状况而定的正常数.现有某种刚泡好的红茶水温度是 , 放在的空气中自然冷却,10分钟以后茶水的温度是 .(1)、求k的值;(2)、经验表明,温度为 的该红茶水放在的空气中自然冷却至时饮用,可以产生最佳口感,那么,大约需要多长时间才能达到最佳饮用口感?(结果精确到0.1,附:参考值)
22. 已知函数(1)、若 , 成立,求实数的取值范围;(2)、证明:有且只有一个零点 , 且 .