北京市通州区2021-2022学年高一上学期数学期末考试试卷
试卷更新日期:2022-07-21 类型:期末考试
一、单选题
-
1. 已知集合 , , 则 ( )A、{-1} B、{1} C、 D、2. 已知 , 则“”是“”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 已知函数 , 则( )A、当且仅当时,有最小值为 B、当且仅当时,有最小值为 C、当且仅当时,有最大值为 D、当且仅当时,有最大值为4. 下列各式中,正确的是( )A、 B、 C、 D、5. 计算( )A、 B、 C、 D、6. 已知函数 , 则的( )A、最小正周期为 , 最大值为 B、最小正周期为 , 最大值为2 C、最小正周期为 , 最大值为 D、最小正周期为 , 最大值为27. 已知函数表示为
0
1
0
-2
设 , 的值域为 , 则( )
A、 , B、 , C、 , D、 ,8. 甲、乙两位同学解答一道题:“已知 , , 求的值.”甲同学解答过程如下:
解:由 , 得.
因为 ,
所以.
所以
.
乙同学解答过程如下:
解:因为 ,
所以
.
则在上述两种解答过程中( )
A、甲同学解答正确,乙同学解答不正确 B、乙同学解答正确,甲同学解答不正确 C、甲、乙两同学解答都正确 D、甲、乙两同学解答都不正确9. 已知函数( , , )的图象如图所示,则( )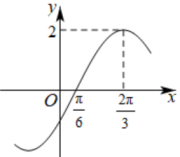 A、 B、对于任意 , , 且 , 都有 C、 , 都有 D、 , 使得10. 已知关于的方程()的根为负数,则的取值范围是( )A、 B、 C、 D、
A、 B、对于任意 , , 且 , 都有 C、 , 都有 D、 , 使得10. 已知关于的方程()的根为负数,则的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 不等式 的解集为 .12. 化简 .13. 某池塘里原有一块浮萍,浮萍蔓延后的面积(单位:平方米)与时间(单位:月)的关系式为(且)图象如图所示. 则下列结论:

①浮萍蔓延每个月增长的面积都相同;
②浮萍蔓延3个月后的面积是浮萍蔓延5个月后的面积的;
③浮萍蔓延每个月增长率相同,都是50%;
④浮萍蔓延到3平方米所经过的时间与蔓延到4平方米所经过的时间的和比蔓延到12平方米所经过的时间少.
其中正确结论的序号是 .
14. 已知 , , 则; .15. 已知 , 且是第三象限角,则; .三、解答题
-
16. 已知二次函数.(1)、求的对称轴;(2)、若 , 求的值及的最值.17. 已知函数 , 且的图象经过点 .(1)、求的值;(2)、求在区间上的最大值;(3)、若 , 求证:在区间内存在零点.18. 如图,在平面直角坐标系中,角的顶点与原点重合,始边与轴的非负半轴重合,终边与单位圆交于点 , .
 (1)、求的值;(2)、将射线绕坐标原点按逆时针方向旋转后与单位圆交于点 , 求的值;(3)、若点与关于轴对称,求的值.19. 已知函数 .(1)、求的最大值,并写出取得最大值时自变量的集合;(2)、把曲线向左平移个单位长度,然后使曲线上各点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,求在上的单调递增区间.20. 某地区每年各个月份的月平均最高气温近似地满足周期性规律,因此第个月的月平均最高气温可近似地用函数来刻画,其中正整数表示月份且 , 例如表示1月份,和是正整数, , . 统计发现,该地区每年各个月份的月平均最高气温基本相同,1月份的月平均最高气温为3摄氏度,是一年中月平均最高气温最低的月份,随后逐月递增直到月份达到最高为33摄氏度.(1)、求的解析式;(2)、某植物在月平均最高气温低于摄氏度的环境中才可生存,求一年中该植物在该地区可生存的月份数.21. 若函数的自变量的取值范围为时,函数值的取值范围恰为 , 就称区间为的一个“和谐区间” .(1)、先判断“函数没有“和谐区间”是否正确,再写出函数的“和谐区间”;(2)、若是定义在上的奇函数,当时,.
(1)、求的值;(2)、将射线绕坐标原点按逆时针方向旋转后与单位圆交于点 , 求的值;(3)、若点与关于轴对称,求的值.19. 已知函数 .(1)、求的最大值,并写出取得最大值时自变量的集合;(2)、把曲线向左平移个单位长度,然后使曲线上各点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象,求在上的单调递增区间.20. 某地区每年各个月份的月平均最高气温近似地满足周期性规律,因此第个月的月平均最高气温可近似地用函数来刻画,其中正整数表示月份且 , 例如表示1月份,和是正整数, , . 统计发现,该地区每年各个月份的月平均最高气温基本相同,1月份的月平均最高气温为3摄氏度,是一年中月平均最高气温最低的月份,随后逐月递增直到月份达到最高为33摄氏度.(1)、求的解析式;(2)、某植物在月平均最高气温低于摄氏度的环境中才可生存,求一年中该植物在该地区可生存的月份数.21. 若函数的自变量的取值范围为时,函数值的取值范围恰为 , 就称区间为的一个“和谐区间” .(1)、先判断“函数没有“和谐区间”是否正确,再写出函数的“和谐区间”;(2)、若是定义在上的奇函数,当时,.(i)求的“和谐区间”;
(ii)若函数的图象是在定义域内所有“和谐区间”上的图象,是否存在实数 , 使集合恰含有2个元素,若存在,求出的取值范围;若不存在,请说明理由.