四川省眉山市仁寿县2022年九校联考数学试卷
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. -8的绝对值是( )A、8 B、-8 C、
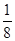 D、
D、 2. 将 用科学记数法表示为( )A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 不等式 的解集是( )A、 B、 C、 D、6. 某班40名同学一周参加体育锻炼时间统计如表所示:
2. 将 用科学记数法表示为( )A、 B、 C、 D、3. 计算 的结果是( )A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 不等式 的解集是( )A、 B、 C、 D、6. 某班40名同学一周参加体育锻炼时间统计如表所示:人数(人)
3
17
13
7
时间(小时)
7
8
9
10
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A、17,8.5 B、17,9 C、8,9 D、8,8.57. 已知 , ,其中 , 为正整数,则 ( )A、 B、 C、 D、8. 红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )A、3种 B、4种 C、5种 D、6种9. 如一次函数 与反比例函数 的图象如图所示,则二次函数 的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:°≈0.73,cos8°≈0.67,tan48°≈1.11)
10. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)=1:2.4的山坡AB上发现有一棵占树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为( )(参考数据:°≈0.73,cos8°≈0.67,tan48°≈1.11)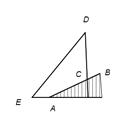 A、17.0米 B、21.9米 C、23.3米 D、33.3米11. 如图是函数y=x2-2x-3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A、17.0米 B、21.9米 C、23.3米 D、33.3米11. 如图是函数y=x2-2x-3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( ) A、 B、 C、 D、或12. 如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC',DC′与AB交于点E,连结AC',若AD=AC′=2,BD=3,则点D到BC′的距离为( )
A、 B、 C、 D、或12. 如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC',DC′与AB交于点E,连结AC',若AD=AC′=2,BD=3,则点D到BC′的距离为( )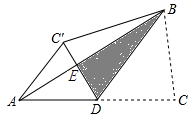 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 方程组 的解是 .14. 分解因式: = .15. 方程 的解是 .16. 如图所示,AB是⊙O的直径,弦 于H, ,则⊙O的半径是 .
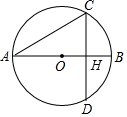 17. 一艘轮船在静水中的最大航速为 , 它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相同,则江水的流速为.18. 某活动小组购买4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为 元,足球的单价为 元,依题意,可列方程组为 .
17. 一艘轮船在静水中的最大航速为 , 它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相同,则江水的流速为.18. 某活动小组购买4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为 元,足球的单价为 元,依题意,可列方程组为 .三、解答题
-
19. 计算:(1)、 ;(2)、20. 某市气象局统计了5月1日至8日中午12时的气温(单位:℃),整理后分别绘制成如图所示的两幅统计图.
根据图中给出的信息,解答下列问题:
 (1)、该市5月1日至8日中午12时气温的平均数是 ℃,中位数是 ℃;(2)、求扇形统计图中扇形A的圆心角的度数 ;(3)、现从该市5月1日至5日的5天中,随机抽取2天,求恰好抽到2天中午12时的气温均低于20℃的概率.21. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)、该市5月1日至8日中午12时气温的平均数是 ℃,中位数是 ℃;(2)、求扇形统计图中扇形A的圆心角的度数 ;(3)、现从该市5月1日至5日的5天中,随机抽取2天,求恰好抽到2天中午12时的气温均低于20℃的概率.21. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.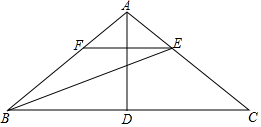 (1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.22. 辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.(1)、求甲、乙两种客房每间现有定价分别是多少元?(2)、度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润m最大,最大利润是多少元?23. 如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作 ,垂足为M,AM与BD相交于点F.求证: .
(1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.22. 辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.(1)、求甲、乙两种客房每间现有定价分别是多少元?(2)、度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润m最大,最大利润是多少元?23. 如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作 ,垂足为M,AM与BD相交于点F.求证: . 24. 如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P显AD上一点,连接CP.
24. 如图,在平行四边形ABCD中,点E在边BC上,连结AE,EM⊥AE,垂足为E,交CD于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P显AD上一点,连接CP. (1)、若DP=2AP=4,CP= , CD=5,求△ACD的面积.(2)、若AE=BN,AN=CE,求证:AD=CM+2CE.25. 如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)、若DP=2AP=4,CP= , CD=5,求△ACD的面积.(2)、若AE=BN,AN=CE,求证:AD=CM+2CE.25. 如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF. (1)、求证:;(2)、若AD=BE=2,求BF的长.26. 如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E.
(1)、求证:;(2)、若AD=BE=2,求BF的长.26. 如图,在平面在角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B(点A在点B的左侧)交y轴于点C,点D为抛物线的顶点,对称轴与x轴交于点E. (1)、连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+PC的最小值;(2)、在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度(0°<<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
(1)、连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当MN取得最大值时,求HF+FP+PC的最小值;(2)、在(1)中,当MN取得最大值HF+FP+1/3PC取得小值时,把点P向上平移个单位得到点Q,连结AQ,把△AOQ绕点O瓶时针旋转一定的角度(0°<<360°),得到△AOQ,其中边AQ交坐标轴于点C在旋转过程中,是否存在一点G使得?若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.