四川省德阳市旌阳区2022年中考一模数学试卷

试卷更新日期：2022-07-21 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2022}$ 相反数的是（）

A、2022 B、 $\frac{1}{2022}$ C、 $\pm \frac{1}{2022}$ D、 $- 2022$

查看试题解析
2. 随着北斗系统全球组网的步伐，北斗芯片的研发生产技术也在逐步成熟，国产北斗芯片可支持接收多系统的导航信号，应用于自动驾驶、无人机、机器人等高精度定位需求领域，将为中国北斗导航产业发展提供有力支持．目前，该芯片工艺已达22纳米（即0.000000022米）．则数据0.000000022用科学记数法表示为（）

A、0.22×10^﹣7 B、2.2×10^﹣8 C、22×10^﹣9 D、22×10^﹣10

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{8}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(- 3 a)}^{2} = 6 a^{2}$ D、 $2 a b^{2} + 3 a b^{2} = 5 a^{2} b^{4}$

查看试题解析
4.
如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　　）

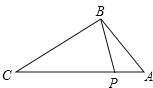A、∠ABP=∠C B、∠APB=∠ABC C、 $\frac{A P}{A B} = \frac{A B}{A C}$ D、 $\frac{A B}{B P} = \frac{A C}{C B}$

查看试题解析
5. 如图，直线 $m / / n$ ，三角尺的直角顶点在直线m上，且三角尺的直角被直线m平分，若 $∠ 1 = 60 °$ ，则下列结论错误的是（）

A、 $∠ 2 = 75 °$ B、 $∠ 3 = 45 °$ C、 $∠ 4 = 105 °$ D、 $∠ 5 = 130 °$

查看试题解析
6. 古代一歌谣：栖树一群鸦，鸦树不知数：三个坐一棵，五个地上落；五个坐一棵，闲了一棵树.请你动脑筋，鸦树各几何？若设乌鸦有x只，树有y棵，由题意可列方程组（）

A、 ${\begin{array}{l} 3 y + 5 = x \\ 5 y - 1 = x \end{array}$ B、 ${\begin{array}{l} 3 y - 5 = x \\ 5 y = x - 1 \end{array}$ C、 ${\begin{array}{l} \frac{1}{3} x + 5 = y \\ 5 y = x - 5 \end{array}$ D、 ${\begin{array}{l} \frac{x - 5}{3} = y \\ \frac{x}{5} = y - 1 \end{array}$

查看试题解析
7. 某校“英语课本剧”表演比赛中，九年级的10名学生参赛成绩统计如图所示，对于这10名学生的参赛成绩，下列说法中正确的是（）

A、平均数是88 B、众数是85 C、中位数是90 D、方差是6

查看试题解析
8. 如图是一个几何体的三视图，根据图中提供的数据，计算这个几何体的表面积是（）

A、 $48 + 60 π$ B、 $48 + 40 π$ C、 $48 + 30 π$ D、 $48 + 36 π$

查看试题解析
9. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F，若⊙O的半径为 $4 \sqrt{3}$ ，∠CDF=15°，则阴影部分的面积为（）

A、 $16 π - 12 \sqrt{3}$ B、 $16 π - 24 \sqrt{3}$ C、 $20 π - 12 \sqrt{3}$ D、 $20 π - 24 \sqrt{3}$

查看试题解析
10. 若数m使关于y的方程 $\frac{1}{y^{2} - y} + \frac{m - 5}{y^{2} + y} = \frac{m - 1}{y^{2} - 1}$ 无解，且使关于x的不等式组 ${\begin{array}{l} \frac{5 x + 3}{2} > x \\ 3 x - 2 m \leq - 2 \end{array}$ 有整数解且至多有4个整数解，则符合条件的m之和为（）

A、 $18$ B、 $15$ C、 $12$ D、 $9$

查看试题解析
11. 将 $△ O B A$ 按如图方式放置在平面直角坐标系 $x O y$ 中，其中 $∠ O B A = 90 °$ ， $∠ A = 30 °$ ，顶点A的坐标为 $(1 ， \sqrt{3})$ ，将 $△ O B A$ 绕原点逆时针旋转，每次旋转60°，则第2022次旋转结束时，点A对应点的坐标为（）

A、 $(- 1 ， \sqrt{3})$ B、 $(1 ， \sqrt{3})$ C、 $(- \frac{\sqrt{3}}{3} ， 1)$ D、 $(- 1 ， \frac{\sqrt{3}}{3})$

查看试题解析
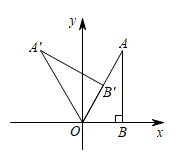12. 抛物线y＝ax²+bx+c的对称轴是直线x＝﹣1，且过点(1，0)，顶点位于第二象限，其部分图象如图所示，给出以下判断：①ab＞0且c＜0；②4a﹣2b+c＞0；③8a+c＞0；④c＝3a﹣3b；⑤直线y＝2x+2与抛物线y＝ax²+bx+c两个交点的横坐标分别为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} + x_{1} \cdot x_{2} = - 5$ 其中正确的选项是（　　）

A、①③ B、①②④ C、②④⑤ D、②③④⑤

查看试题解析

二、填空题

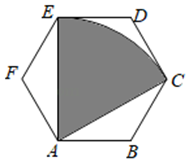
13. 分解因式：﹣x²y＋6xy﹣9y＝．

查看试题解析
14. “平行四边形的对角线互相垂直平分”是事件.（填“必然”“不可能”或“随机”）

查看试题解析
15. 如图，正六边形 $A B C D E F$ 的边长为2，以 $A$ 为圆心， $A C$ 的长为半径画弧，得 $\overset{⌢}{E C}$ ，连接 $A C$ ， $A E$ ，则图中阴影部分的面积为．

查看试题解析
16. 如图，在菱形 $A B C D$ 中， $A B = A C = 10$ ，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，点 $M$ 在线段 $A C$ 上，且 $A M = 3$ ，点 $P$ 为线段 $B D$ 上的一个动点，则 $M P + \frac{1}{2} P B$ 的最小值是.

查看试题解析
17. 如图，点A、B在双曲线y＝ $\frac{k}{x}$ （x＞0）上，点C、D在坐标轴上，AC⊥x轴，BD⊥y轴，OA与BD交于点E，OB与AC交于点F，AC与DB交于点G，BD＝2OC，四边形OEGF的面积为2，则k的值为．

查看试题解析
18. 已知二次函数 $y = x^{2} - 2 (k + 1) x + k^{2} - 2 k - 3$ 与x轴有两个交点，把当k取最小整数时的二次函数的图象在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象，若新图象与直线 $y = x + m$ 有三个不同的公共点，则m的值为.

查看试题解析

三、解答题

19. $6 \sin 45 ° + | 1 - \sqrt{2} | - \sqrt{8} \times {(π - 2022)}^{0} - {(\frac{1}{2})}^{- 2}$ .

查看试题解析
20. 为落实“双减”，进一步深化白云区“数学提升工程”，提升学生数学核心素养，2021年12月3日开展“双减”背景下白云区初中数学提升工程成果展示现场会，其中活动型作业展示包括以下项目：①数独挑战；②数学谜语；③一笔画；④24点；⑤玩转魔方.为了解学生最喜爱的项目，随机抽取若干名学生进行调查，将调查结果绘制成两个不完整的统计图，如图：

(1)、本次随机抽查的学生人数为人，补全图（Ⅰ）；

(2)、参加活动的学生共有500名，可估计出其中最喜爱①数独挑战的学生人数为人，图（Ⅱ）中扇形①的圆心角度数为度；

(3)、计划在①，②，③，④四项活动中随机选取两项作为重点直播项日，请用列表或画树状图的方法，求恰好选中①，④这两项活动的概率

查看试题解析
21. 如图，点E是平行四边形 $A B C D$ 对角线 $A C$ 上一点，点F在 $B E$ 延长线上，且 $E F = B E$ ， $E F$ 与 $C D$ 交于点G.

(1)、求证：DF//AC；

(2)、连接 $D E$ 、 $C F$ ，若 $2 A B = B F$ ， G恰好是 $C D$ 的中点，求证：四边形 $C F D E$ 是矩形.

查看试题解析
22. 如图，已知反比例函数 $y = \frac{m}{x}$ 的图象与正比例函数y＝nx的图象相交于点A（2，﹣2）和点B.

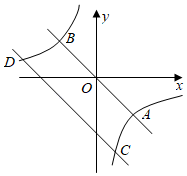(1)、求正比例函数和反比例函数的解析式；

(2)、将直线AB向下平移3个单位长度，与反比例函数的图象相交于点C和点D.
①求点C的坐标；
②点P是x轴上一点，当线段PC与线段PA之差达到最大时，求点P的坐标.

查看试题解析

23. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克.

营养品信息表
营养成分	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
A包装	1千克	45元
B包装	0.25千克	12元

(1)、问甲、乙两种食材每千克进价分别是多少元？

(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出.若A的数量不低于B的数量，则A为多少包时，每日所获总利润最大？最大总利润为多少元？

查看试题解析

24. 如图，在△ABC中， $A C = B C$ ，以C为直径作⊙O，交AC于点M，作 $C D ⊥ A C$ 交AB延长线于点D，E为CD上一点，且 $B E = D E$ .

(1)、求证：BE为⊙O的切线；

(2)、若 $A M = 4$ ， $t a n A = 2$ ，求DE的长.

查看试题解析
25. 如图，把两个全等的 $R t △ A O B$ 和 $R t △ C O D$ 分别置于平面直角坐标系中，使直角边OB、OD在x轴上.已知点 $A (2 ， 4)$ ，过A、C两点的直线分别交x轴、y轴于点E、F，抛物线 $y = a x^{2} + b x + c$ 经过O、A、C三点.

(1)、求该抛物线的函数解析式；

(2)、点G为抛物线上位于线段OC所在直线上方部分的一动点，求G到直线OC的最大距离和此时点G的坐标；

(3)、点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM的边AM与边BP相等？若存在，求出此时点P的坐标；若不存在，请说明理由.

查看试题解析