陕西省榆林市2022年初中学业水平模拟考试数学试卷
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. 计算:( )A、 B、1 C、-1 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , 与交于点O,连接 , 若 , , 则的度数是( )
3. 如图, , 与交于点O,连接 , 若 , , 则的度数是( )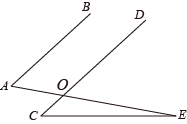 A、15° B、20° C、10° D、25°4. 化简的结果是( )A、 B、 C、 D、5. 如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A、15° B、20° C、10° D、25°4. 化简的结果是( )A、 B、 C、 D、5. 如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( ) A、4 B、3 C、2 D、16. 把正比例函数的图象向下平移3个单位,则下列各坐标所表示的点中,在平移后的函数图象上的是( )A、 B、 C、 D、7. 如图,AB为⊙O的直径,AB=4,弦CD=2 , 则劣弧的长为( )
A、4 B、3 C、2 D、16. 把正比例函数的图象向下平移3个单位,则下列各坐标所表示的点中,在平移后的函数图象上的是( )A、 B、 C、 D、7. 如图,AB为⊙O的直径,AB=4,弦CD=2 , 则劣弧的长为( )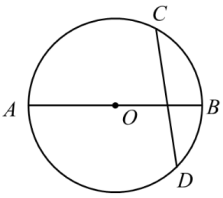 A、 B、 C、 D、8. 已知二次函数的图象经过原点,它可以由二次函数的图象平移得到,则a的值是( )A、4 B、-2 C、2 D、1
A、 B、 C、 D、8. 已知二次函数的图象经过原点,它可以由二次函数的图象平移得到,则a的值是( )A、4 B、-2 C、2 D、1二、填空题
-
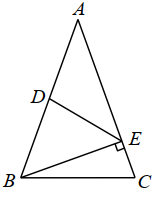
9. 写出一个无理数x,使得 , 则x可以是.(只要写出一个满足条件的x即可)10. 若正多边形的内角和是540°,则该正多边形的一个外角为°.11. 如图,中, , D为中点,E在上,且 , 若 , , 则边的长度为.
 12. 如图,反比例函数的图象与一次函数y=﹣2x+3的图象相交于点P,点P到y轴的距离是1,则这个反比例函数的解析式是.
12. 如图,反比例函数的图象与一次函数y=﹣2x+3的图象相交于点P,点P到y轴的距离是1,则这个反比例函数的解析式是.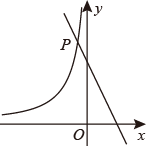 13. 如图,在中, , , 点P是斜边上任意一点,D是的中点,连接并延长,使.以 , 为边构造平行四边形 , 则对角线的最小值为.
13. 如图,在中, , , 点P是斜边上任意一点,D是的中点,连接并延长,使.以 , 为边构造平行四边形 , 则对角线的最小值为.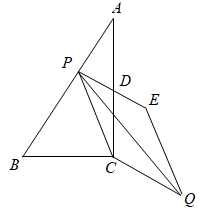
三、解答题
-
14. 计算:.15. 计算:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2.16. 解不等式组 ,并写出它的最大负整数解.17. 如图,在△ABC中,DE⊥BC于点D,交AB于点E.请用尺规作图法,在线段DC上求作一点P,使AP∥ED.(保留作图痕迹,不写作法)
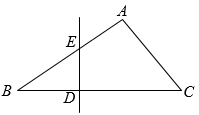 18. 如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
18. 如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.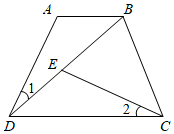 19. 北京冬奥会之所以能够开启全球冰雪运动新时代,关键在于中国通过筹办冬奥会和推广冬奥运动,让冰雪运动进入寻常百姓家.某校组建了一个滑雪队,现队长需要购买一些滑雪板,经了解,现有A、B两种滑雪板若购买2副A种滑雪板和1副B种滑雪板共需340元;若购买3副A种滑雪板和2副B种滑雪板共需570元.求1副A种滑雪板和1副B种滑雪板各是多少元?20. 扑克牌在生活中很常见,一副扑克牌共有54张,对它们的解释也非常奇妙:大王代表太阳、小王代表月亮,其余52张牌代表一年中的52个星期;红桃、方块、梅花、黑桃四种花色分别象征着春、夏、秋、冬四个季节.扑克牌的设计和发明与天文、历法有着千丝万缕的联系.小云将一副扑克牌中的红桃2、方块3、梅花4、黑桃5这四张牌的背面朝上.(1)、洗匀后从中任意翻开一张,求翻开的牌是红桃2的概率;(2)、洗匀后从四张牌中同时任意翻开两张,用画树状图或列表的方法,求翻开的两张牌分别象征春季、冬季的概率.21. 镇北台位于陕西省榆林城北4公里之红山顶上.据险临下,控南北之咽喉,如巨锁扼边关要隘,为古长城沿线现存最大的要塞之一.某“综合与实践”小组开展了测量镇北台高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量、如图,他们先在镇北台底部所在的平地上,放置一个平面镜E,甲同学后退到点D时,刚好从镜子中看到镇北台的顶端点A的像,测得 , 甲同学的眼睛到地面的距离为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高 , .已知 , , , 点B、E、D、F在一条直线上,请你求出镇北台的高度.
19. 北京冬奥会之所以能够开启全球冰雪运动新时代,关键在于中国通过筹办冬奥会和推广冬奥运动,让冰雪运动进入寻常百姓家.某校组建了一个滑雪队,现队长需要购买一些滑雪板,经了解,现有A、B两种滑雪板若购买2副A种滑雪板和1副B种滑雪板共需340元;若购买3副A种滑雪板和2副B种滑雪板共需570元.求1副A种滑雪板和1副B种滑雪板各是多少元?20. 扑克牌在生活中很常见,一副扑克牌共有54张,对它们的解释也非常奇妙:大王代表太阳、小王代表月亮,其余52张牌代表一年中的52个星期;红桃、方块、梅花、黑桃四种花色分别象征着春、夏、秋、冬四个季节.扑克牌的设计和发明与天文、历法有着千丝万缕的联系.小云将一副扑克牌中的红桃2、方块3、梅花4、黑桃5这四张牌的背面朝上.(1)、洗匀后从中任意翻开一张,求翻开的牌是红桃2的概率;(2)、洗匀后从四张牌中同时任意翻开两张,用画树状图或列表的方法,求翻开的两张牌分别象征春季、冬季的概率.21. 镇北台位于陕西省榆林城北4公里之红山顶上.据险临下,控南北之咽喉,如巨锁扼边关要隘,为古长城沿线现存最大的要塞之一.某“综合与实践”小组开展了测量镇北台高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量、如图,他们先在镇北台底部所在的平地上,放置一个平面镜E,甲同学后退到点D时,刚好从镜子中看到镇北台的顶端点A的像,测得 , 甲同学的眼睛到地面的距离为1.5m;然后,利用测角仪在点F处测得镇北台的顶端点A的仰角为45°,测角仪的高 , .已知 , , , 点B、E、D、F在一条直线上,请你求出镇北台的高度. 22. 据悉,2022年,我国载人航天空间站工程进人空间站建造阶段,将完成问天实验舱、梦天实验舱、神舟载人飞船和天舟货运飞船等6次重大任务.为了庆祝我国航天事业的蓬勃发展,某校举办名为“弘扬航天精神·拥抱星辰大海”的书画展览,并给书画展上的作品打分(满分10分),评分结果有6分,7分,8分,9分,10分五种.每位同学只能上交一份作品,现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.根据以上信息,解答下列问题:
22. 据悉,2022年,我国载人航天空间站工程进人空间站建造阶段,将完成问天实验舱、梦天实验舱、神舟载人飞船和天舟货运飞船等6次重大任务.为了庆祝我国航天事业的蓬勃发展,某校举办名为“弘扬航天精神·拥抱星辰大海”的书画展览,并给书画展上的作品打分(满分10分),评分结果有6分,7分,8分,9分,10分五种.每位同学只能上交一份作品,现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.根据以上信息,解答下列问题: (1)、补全条形统计图;(2)、求所抽取作品成绩的众数、中位数和平均数(结果保留一位小数);(3)、已知该校收到书画作品共900份,请估计得分为10分的书画作品大约有多少份?23. 万物复苏必有时,疫去安来春可期.某地爆发新一波的疫情,疫情期间为保障市民正常生活,现要用10辆汽车装运蔬菜和水果到该地,每辆汽车只能装运同一种物资且必须装满,根据表中提供的信息,解答下列问题:
(1)、补全条形统计图;(2)、求所抽取作品成绩的众数、中位数和平均数(结果保留一位小数);(3)、已知该校收到书画作品共900份,请估计得分为10分的书画作品大约有多少份?23. 万物复苏必有时,疫去安来春可期.某地爆发新一波的疫情,疫情期间为保障市民正常生活,现要用10辆汽车装运蔬菜和水果到该地,每辆汽车只能装运同一种物资且必须装满,根据表中提供的信息,解答下列问题:物资种类
蔬菜
水果
每辆汽车运载量/吨
m
m-2
每吨所需运费/元
120
100
已知1辆车所装蔬菜的质量与2辆车所装水果的质量之和为14吨.
(1)、求m的值;(2)、设装运蔬菜的车辆有x辆,运输这批物资所需总运费为y元,求y与x之间的函数关系,并求当装运蔬菜的车辆不少于装运水果的车辆的2倍时,至少需要总运费多少元?24. 如图,是的外接圆,为的直径,过点C作的切线 , 交的延长线于点D.过点O作 , 交的延长线于点E.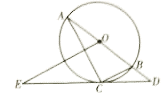 (1)、求证:;(2)、若 , , 求的半径.25. 已知抛物线过点 , 两点,点C、B关于抛物线的对称轴对称.(1)、求该抛物线的函数表达式;(2)、点Q是y轴上一动点,在抛物线上是否存在点P,使得以点B、C,P、Q为顶点的四边形是平行四边形,若存在,请求出点P的坐标,若不存在,请说明理由.26.
(1)、求证:;(2)、若 , , 求的半径.25. 已知抛物线过点 , 两点,点C、B关于抛物线的对称轴对称.(1)、求该抛物线的函数表达式;(2)、点Q是y轴上一动点,在抛物线上是否存在点P,使得以点B、C,P、Q为顶点的四边形是平行四边形,若存在,请求出点P的坐标,若不存在,请说明理由.26.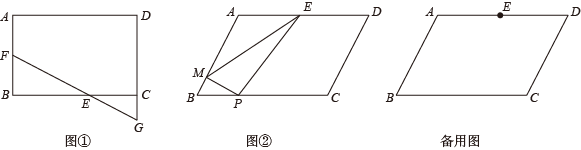 (1)、问题提出
(1)、问题提出
如图①,在矩形中, , , 点F是的中点,点E在上, , 连接并延长交的延长线于点G,求的长;(2)、问题解决
如图②,某生态农庄有一块形状为平行四边形的土地,其中 , , .管理者想规划出一个形状为的区域建成亲子采摘中心,根据设计要求,点E是的中点,点P、M分别在、上,.设的长为 , 的面积为.①求y与x之间的函数关系式;
②为容纳更多的游客,要求的面积尽可能的大,请求出面积的最大值,并求出此时的长.