陕西省宝鸡市岐山县2022年九年级第一次模拟考试数学试卷
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2022 B、 C、2022 D、2. 下图是赵凯同学绘制的疫情防控宣传图标,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 据报道,在新冠疫苗的防重症保护效力下,德尔塔毒株的“突破性感染”占比约为0.00098,将0.00098用科学记数法表示为( )A、 B、 C、 D、4. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )
3. 据报道,在新冠疫苗的防重症保护效力下,德尔塔毒株的“突破性感染”占比约为0.00098,将0.00098用科学记数法表示为( )A、 B、 C、 D、4. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )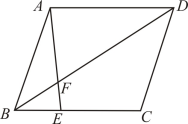 A、 B、 C、 D、5. 在平面直角坐标系中,将直线沿y轴向下平移6个单位后,得到一条新的直线,该直线与x轴的交点坐标是( )A、 B、 C、 D、6. 如图,与相切于点B,连接交于点C,D为优弧上一点,连接 , , 若 , 则的度数为( )
A、 B、 C、 D、5. 在平面直角坐标系中,将直线沿y轴向下平移6个单位后,得到一条新的直线,该直线与x轴的交点坐标是( )A、 B、 C、 D、6. 如图,与相切于点B,连接交于点C,D为优弧上一点,连接 , , 若 , 则的度数为( )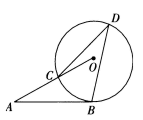 A、20° B、30° C、35° D、55°7. 在平面直角坐标系内,抛物线与x轴的一个交点是 , 另一交点为B,则的长为( )A、2 B、3 C、6 D、88. 如图,在正方形中有两个正方形,如果记正方形的面积为 , 正方形的面积为 , 则和的关系为( )
A、20° B、30° C、35° D、55°7. 在平面直角坐标系内,抛物线与x轴的一个交点是 , 另一交点为B,则的长为( )A、2 B、3 C、6 D、88. 如图,在正方形中有两个正方形,如果记正方形的面积为 , 正方形的面积为 , 则和的关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 分解因式:.10. 若菱形的边长为10,内角 , 则菱形的面积为.11. 如图所示的圆球三角垛自上而下,第1层1个,第2层个,第3层个,……如果图中三角垛共6层,则这个圆球三角垛的最下方一层的圆球个数为个.
 12. 已知反比例函数(k为常数)的图象上有三点分别是、、 , 则三个点横坐标的大小关系是.(用>号连接)13. 如图,在四边形中, , , , 若四边形是菱形,则的值为.
12. 已知反比例函数(k为常数)的图象上有三点分别是、、 , 则三个点横坐标的大小关系是.(用>号连接)13. 如图,在四边形中, , , , 若四边形是菱形,则的值为.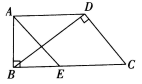
三、解答题
-
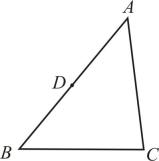
14. 计算:.15. 解不等式组: .16. 化简:.17. 如图,在中,为边的中点,请用尺规作图法求作线段 , 使得点E在上, , 且.(保留作图痕迹,不写作法)
 18. 如图,在四边形中, , E、F分别是、边上的中点,且.求证:.
18. 如图,在四边形中, , E、F分别是、边上的中点,且.求证:. 19. 某医疗器械企业计划购进20台机器生产口罩,已知生产口罩面的机器每台每天的产量为12000个,生产耳挂绳的机器每台每天的产量为96000个,口罩是一个口罩面和两个耳挂绳构成,为使每天生产的口罩面和耳挂绳刚好配套,该企业应分别购进生产口罩面和生产耳挂绳的机器各多少台?20. 2022年冬奥会和残奥会相继在北京举行,两场体育盛会的吉祥物“冰墩墩”和“雪容融”广受大众喜爱,甚至多地出现“一墩难求”的现象.某玩具超市趁机推出吉祥物盲盒让顾客随机购买,小丽到盲盒区时仅剩最后四个盲盒,它们的形状外观大小完全一样,已知四个盲盒中有两个装有冬奥会吉祥物“冰墩墩”玩偶(记作 , ),有一个装有残奥会吉祥物“雪容融”玩偶(记作B),还有一个装有虎年特制的小老虎玩偶(记作C).(1)、随机购买一个盲盒,恰好买到“冰墩墩”玩偶的概率是.(2)、请利用树状图或列表法,求小丽购买其中两个盲盒,里面恰好是一个“冰墩墩”玩偶和一个“雪容融”玩偶的概率.21. 如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部垂直于墙面 , 床紧靠墙面放置,当导风板所在的直线与竖直直线的夹角时,空调风刚好吹到床的外边沿E处,于点D,于点F.若 , , 床铺 , 求空调挂机的底部位置距离床的高度.(参考数据: , , )
19. 某医疗器械企业计划购进20台机器生产口罩,已知生产口罩面的机器每台每天的产量为12000个,生产耳挂绳的机器每台每天的产量为96000个,口罩是一个口罩面和两个耳挂绳构成,为使每天生产的口罩面和耳挂绳刚好配套,该企业应分别购进生产口罩面和生产耳挂绳的机器各多少台?20. 2022年冬奥会和残奥会相继在北京举行,两场体育盛会的吉祥物“冰墩墩”和“雪容融”广受大众喜爱,甚至多地出现“一墩难求”的现象.某玩具超市趁机推出吉祥物盲盒让顾客随机购买,小丽到盲盒区时仅剩最后四个盲盒,它们的形状外观大小完全一样,已知四个盲盒中有两个装有冬奥会吉祥物“冰墩墩”玩偶(记作 , ),有一个装有残奥会吉祥物“雪容融”玩偶(记作B),还有一个装有虎年特制的小老虎玩偶(记作C).(1)、随机购买一个盲盒,恰好买到“冰墩墩”玩偶的概率是.(2)、请利用树状图或列表法,求小丽购买其中两个盲盒,里面恰好是一个“冰墩墩”玩偶和一个“雪容融”玩偶的概率.21. 如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部垂直于墙面 , 床紧靠墙面放置,当导风板所在的直线与竖直直线的夹角时,空调风刚好吹到床的外边沿E处,于点D,于点F.若 , , 床铺 , 求空调挂机的底部位置距离床的高度.(参考数据: , , )

图1 图2
22. 为了倡导同学们了解掌握节能降耗、科学用电,王蜂所在的学习小组在社区随机抽取调查部分家庭每天的用电情况,将调查数据进行如下整理,并绘制了不完整的统计表.每天用电量(kW·h)分组
频数(户)
频率
各组每天用电总量(kW·h)
4
0.08
8
14
0.28
70
16
n
128
m
0.12
60
10
0.2
134
根据以上提供的信息,解答下列问题:
(1)、填空: , .(2)、求被调查家庭的每天用电量的平均数.(3)、若该社区共有3000户家庭,电价为0.6元/kW·h,根据调查数据,请你估计该社区平均每天所支付的总电费为多少元?23. 2021年12月,西安发生疫情,各地纷纷支援.宝鸡迅速组织500名医护人员和抗疫物资星夜出征行驶280km驰援西安同心抗疫.如图,运输防疫物资的货车和载有医护人员的客车先后从宝鸡出发驶向西安,线段表示货车离出发地宝鸡的距离与时间之间的函数关系,折线表示客车离出发地宝鸡的距离与时间之间的函数关系. (1)、载有医护人员的客车中途在高速服务站休息了一段时间,休息时间为h.(2)、求线段对应的函数关系式.(3)、客车从宝鸡出发后经过多长时间追上货车.24. 如图,四边形内接于 , , 为的直径,过D作的切线.
(1)、载有医护人员的客车中途在高速服务站休息了一段时间,休息时间为h.(2)、求线段对应的函数关系式.(3)、客车从宝鸡出发后经过多长时间追上货车.24. 如图,四边形内接于 , , 为的直径,过D作的切线.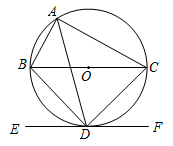 (1)、求证:.(2)、若的半径为5, , 求的长.25. 已知抛物线与y轴的交点为A,顶点为P,对称轴为直线m.(1)、求抛物线l的顶点坐标P和对称轴.(2)、抛物线l关于点A对称的抛物线为 , 抛物线的顶点为Q,对称轴为直线n,在直线m和直线n上是否分别存在点E、F,使得四边形为正方形?若存在,请求出a的值;若不存在,请说明理由.26. 问题提出
(1)、求证:.(2)、若的半径为5, , 求的长.25. 已知抛物线与y轴的交点为A,顶点为P,对称轴为直线m.(1)、求抛物线l的顶点坐标P和对称轴.(2)、抛物线l关于点A对称的抛物线为 , 抛物线的顶点为Q,对称轴为直线n,在直线m和直线n上是否分别存在点E、F,使得四边形为正方形?若存在,请求出a的值;若不存在,请说明理由.26. 问题提出 (1)、如图1,在四边形中, , , , , 将绕点D逆时针旋转90°得.
(1)、如图1,在四边形中, , , , , 将绕点D逆时针旋转90°得.①求线段的长;
②求点E到的距离.
(2)、如图2,为积极响应北京冬奥会“三亿人上冰雪”,让冰雪运动走向大众,某地利用山谷坡地准备建造一处滑雪场地 , 按设计要求,在上选一点E,修建格挡和 , 使且 , 为工作区,为热身试滑区域.已知 , , .请问是否存在符合设计要求的面积最大的热身试滑区域?若存在,求出面积的最大值及此时的长;若不存在,请说明理由.