广西壮族自治区南宁市部分地区2022年九年级下学期3月月考数学试题(一模)
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. 计算( )A、 B、6 C、 D、2. 如图,a,b相交于点O,若 , 则的度数是( )
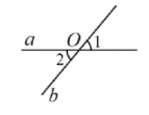 A、40° B、50° C、130° D、135°3. 不等式的解集在数轴上表示正确的是( )A、
A、40° B、50° C、130° D、135°3. 不等式的解集在数轴上表示正确的是( )A、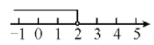 B、
B、 C、
C、 D、
D、 4. 下图是一个几何体的展开图,该几何体是( )
4. 下图是一个几何体的展开图,该几何体是( ) A、圆柱体 B、四棱柱 C、三棱锥 D、圆锥体5. 某种苹果的售价是m元/kg(),现用100元买5kg这种苹果,应找回( )A、元 B、元 C、元 D、元6. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的是72°,那么光线与纸板左上方所成的的度数是( )
A、圆柱体 B、四棱柱 C、三棱锥 D、圆锥体5. 某种苹果的售价是m元/kg(),现用100元买5kg这种苹果,应找回( )A、元 B、元 C、元 D、元6. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的是72°,那么光线与纸板左上方所成的的度数是( )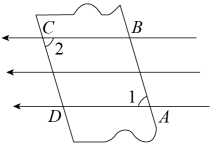 A、18° B、70° C、72° D、108°7. 下列函数图象中,表示直线的是( )A、
A、18° B、70° C、72° D、108°7. 下列函数图象中,表示直线的是( )A、 B、
B、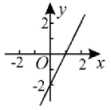 C、
C、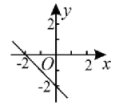 D、
D、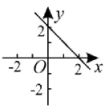 8. 下列运算正确的是( )A、 B、 C、 D、9. 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( )A、 B、 C、 D、10. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )
8. 下列运算正确的是( )A、 B、 C、 D、9. 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( )A、 B、 C、 D、10. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( ) A、 B、 C、 D、11. 《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶盖材料的木杆)设这批椽的数量为株,则符合题意的方程是( )
A、 B、 C、 D、11. 《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶盖材料的木杆)设这批椽的数量为株,则符合题意的方程是( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,点为坐标原点,菱形的顶点的横坐标为3.反比例函数的图象经过点 , 连接 , 过点作交轴于点 , 则的值是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,点为坐标原点,菱形的顶点的横坐标为3.反比例函数的图象经过点 , 连接 , 过点作交轴于点 , 则的值是( )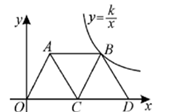 A、12 B、20 C、30 D、32
A、12 B、20 C、30 D、32二、填空题
-
13. ﹣2的相反数的值等于 .14. 若分式 有意义,则 的取值范围是.15. 如图,在平面直角坐标系中,等腰的底边在x轴上,顶点B在y轴上,若点 , 则点A的坐标为.
 16. 如图是某天游玩南宁青秀山的学生人数统计图.若大学生有360人,则初中生有人.
16. 如图是某天游玩南宁青秀山的学生人数统计图.若大学生有360人,则初中生有人.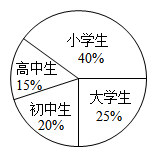 17. 如图,在面积为20的中, , .M为边上一点,将沿所在直线折叠,点A的对应点为 , 若于点H,则图中阴影部分(四边形)的面积为.
17. 如图,在面积为20的中, , .M为边上一点,将沿所在直线折叠,点A的对应点为 , 若于点H,则图中阴影部分(四边形)的面积为. 18. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记 , 则其面积.这个公式也被称为海伦—秦九韶公式.若 , , 则此三角形面积的最大值是.
18. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记 , 则其面积.这个公式也被称为海伦—秦九韶公式.若 , , 则此三角形面积的最大值是.三、解答题
-
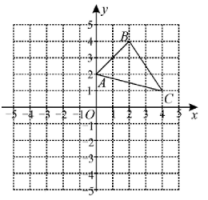
19. 计算: .20. 解方程组:.21. 如图,在平面直角坐标系中,的三个顶点坐标分别是 , , .
 (1)、将向左平移4个单位长度后得到 , 请画出;(2)、以点O为位似中心,在y轴的左侧画出的位似图形 , 使与的位似比为1:2;(3)、请直接写出的值.22. 2019年1月1日,“学习强国”学习平台在全国上线,它是由中共中央宣传部主管,以习近平新时代中国特色社会主义思想和党的十九大精神为主要内容,立足全体党员、面向全社会的优质平台.现某校有教职工400人,党支部通过“问卷星”对该校全体共产党员教职工(以下简称“党员”)在“学习强国”平台学习的时间进行调研(学习时长超过60分钟的统计在范围内)﹒调研结果如下:
(1)、将向左平移4个单位长度后得到 , 请画出;(2)、以点O为位似中心,在y轴的左侧画出的位似图形 , 使与的位似比为1:2;(3)、请直接写出的值.22. 2019年1月1日,“学习强国”学习平台在全国上线,它是由中共中央宣传部主管,以习近平新时代中国特色社会主义思想和党的十九大精神为主要内容,立足全体党员、面向全社会的优质平台.现某校有教职工400人,党支部通过“问卷星”对该校全体共产党员教职工(以下简称“党员”)在“学习强国”平台学习的时间进行调研(学习时长超过60分钟的统计在范围内)﹒调研结果如下:时间(分钟)
人数
10
70
50
60
45
15
(1)、直接写出该校党员在教职工中所占百分比及在平台学习时间的众数出现的范围;(2)、求该校党员使用“学习强国”平台学习的平均时间;(3)、使用平台学习会得到相应的积分,学校拟在拥有积分超5.3万分的4位老师(分别用代号“甲”“乙”“丙”“丁”表示)中随机选两位老师出来在教职工大会上分享学习经验,请用树状图或列表法求出恰好选中“甲”“丙”两位老师的概率.23. 有两个人患了流感,经过两轮传染后共有242人患了流感. (1)、每轮传染中平均一个人传染了几个人?(2)、若一个患流感的人打一个喷嚏喷出的病毒粒子(忽略触角近似于球体)达8000万个,且该流感病毒粒子的直径为160纳米.请完成下列填空及问题:
(1)、每轮传染中平均一个人传染了几个人?(2)、若一个患流感的人打一个喷嚏喷出的病毒粒子(忽略触角近似于球体)达8000万个,且该流感病毒粒子的直径为160纳米.请完成下列填空及问题:①用科学记数法表示数据8000万个为 个;
②如图,若把8000万个病毒粒子最大纵切面圆面相切放在一条直线上,求这些病毒粒子纵切面的总直径是多少米?(参考数据:1纳米米)
24. 已知抛物线.(1)、当时,求抛物线对称轴及与x轴的交点坐标;(2)、①无论为何值,抛物线一定经过两个定点,请直接写出两个定点的坐标;②将抛物线沿这两个定点所在直线翻折,得到抛物线 , 直接写出抛物线的解析式并求出抛物线与抛物线两个顶点的距离;
(3)、若(2)中抛物线的顶点到轴的距离为2,求的值.25. 甲、乙两个“综合与实践”小组计划开展测量某广场同一旗杆高度的实践活动.他们分别制订了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,小组在测量时,对每个数据都分别测量了两次并取它们的平均值作为测量结果,以下是他们研究报告的部分记录内容.
课题
测量旗杆的高度
工具
测角仪,皮尺,镜子等
成员
甲组
乙组
测量说明
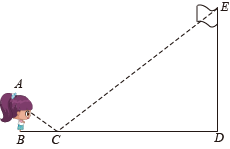
线段表示旗杆,测角仪高度 , 测点A,B与H在地面同一直线上,A,B之间的距离可以测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在上.
线段表示旗杆,镜子放在点C处,人的眼睛与地面距离 , 在测量过程中保证人的眼睛恰好能在镜子中看到旗杆的顶端E.
测量示意图

测量数据
测量项目
第一次
第二次
平均值
测量项目
第一次
第二次
平均值
的度数
26.5°
26.7°
26.6°
B,C之间的距离
1.9m
2.1m
2m
的度数
40.4°
39.6°
40°
C,D之间的距离
25.2m
26.8m
26m
A,B之间的距离
14.4m
14.6m
请完成以下问题:
(1)、表中m;(2)、乙组这种测量方法的原理是我们所学的( )A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似(3)、根据以上测量结果,请帮甲组求出旗杆的高度.(结果精确到0.1)(参考数据: , , , , , )
(4)、经计算乙组测量的结果为19.5米,与甲组的数据有差异,老师说:“你们做得都很好,在我们这种测量条件下,出现误差是事件,所以虽然数据存在差异但数据都是可信的!”(填“必然”,“随机”,“不可能”)26. 如图,点C在以为直径的半圆上, , , 点D在线段上运动,点E与点D关于对称,于点D,并交的延长线于点F.
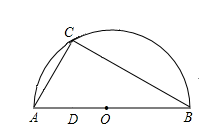 (1)、求证:;(2)、证明:当线段最短时,与半圆相切;(3)、当点F恰好落在上时,求的长度.
(1)、求证:;(2)、证明:当线段最短时,与半圆相切;(3)、当点F恰好落在上时,求的长度.