广西玉林市2022届九年级下学期期中考试数学试题(一模)
试卷更新日期:2022-07-21 类型:中考模拟
一、单选题
-
1. 10的相反数是( )A、-10 B、10 C、 D、2. 如图所示的图形为四位同学画的数轴,其中正确的是( )A、
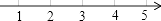 B、
B、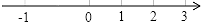 C、
C、 D、
D、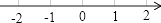 3. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
3. 如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )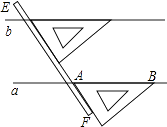 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等4. 下列运算正确的是( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,则该几何体可能是( )
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等4. 下列运算正确的是( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,则该几何体可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 矩形具有而一般的平行四边形不一定具有的特征( )A、对角相等 B、对角线相等 C、对角线互相平分 D、对边相等7. 观察下列图案,其中旋转角最大的是( )A、
6. 矩形具有而一般的平行四边形不一定具有的特征( )A、对角相等 B、对角线相等 C、对角线互相平分 D、对边相等7. 观察下列图案,其中旋转角最大的是( )A、 B、
B、 C、
C、 D、
D、 8. 在学校举办的学习强国演讲比赛中,李华根据九位评委所给的分数制作了如下表格:
8. 在学校举办的学习强国演讲比赛中,李华根据九位评委所给的分数制作了如下表格:平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、平均数 B、众数 C、方差 D、中位数9. 若函数是正比例函数,则m的值是( )A、m=1 B、m=-2 C、m=2 D、m>-210. 如图,在平面直角坐标系xOy中,已知点 , B(2,2).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( ) A、向左平移2个单位,再向下平移2个单位 B、向左平移个单位,再向上平移2个单位 C、向右平移2个单位,再向上平移2个单位 D、向右平移个单位,再向上平移2个单位11. 已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线 , 、是抛物线上的点,是直线l上的点,且 , , 则、、的大小关系为
A、向左平移2个单位,再向下平移2个单位 B、向左平移个单位,再向上平移2个单位 C、向右平移2个单位,再向上平移2个单位 D、向右平移个单位,再向上平移2个单位11. 已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线 , 、是抛物线上的点,是直线l上的点,且 , , 则、、的大小关系为 A、 B、 C、 D、12. 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
A、 B、 C、 D、12. 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )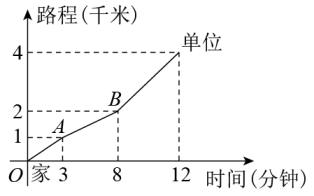 A、12分钟 B、14分钟 C、15分钟 D、20分钟
A、12分钟 B、14分钟 C、15分钟 D、20分钟二、填空题
-
13. 计算:.14. 分解因式:=.15. 如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=60°,则∠ACB=.
 16. 从-2,-1,1,2四个数中,随机抽取两个数相乘,积为大于-4且小于-1的概率是.17. 如图,两个反比例函数(其中)和在第一象限内的图象依次是和 , 点P在上.矩形PCOD交于A,B两点,OA的延长线交于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为9,则EF∶AC为.
16. 从-2,-1,1,2四个数中,随机抽取两个数相乘,积为大于-4且小于-1的概率是.17. 如图,两个反比例函数(其中)和在第一象限内的图象依次是和 , 点P在上.矩形PCOD交于A,B两点,OA的延长线交于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为9,则EF∶AC为. 18. 如图,已知在Rt△ABC中, , 在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2022个内接正方形的边长为.
18. 如图,已知在Rt△ABC中, , 在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD,PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2022个内接正方形的边长为.
三、解答题
-
19. 计算:.20. 先化简,再求值: ,其中 .21. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、若该方程的两个根都是整数,写出一个符合条件的 的值,并求此时方程的根.22. 某中学需在短跑、长跑、跳远、跳高四类体育项目中各选拔一名同学参加市中学生运动会.根据平时成绩,把各项目进入复选的学生情况绘制成如下不完整的统计图:
 (1)、参加复选的学生总人数为人,扇形统计图中短跑项目所对应圆心角的度数为°;(2)、补全条形统计图,并标明数据;(3)、求在跳高项目中男生被选中的概率.23. 如图,AB是⊙O的直径,CD切⊙O于点D,且 , 连接AC.
(1)、参加复选的学生总人数为人,扇形统计图中短跑项目所对应圆心角的度数为°;(2)、补全条形统计图,并标明数据;(3)、求在跳高项目中男生被选中的概率.23. 如图,AB是⊙O的直径,CD切⊙O于点D,且 , 连接AC. (1)、求证:AC是⊙O的切线;(2)、若AB=OC=8,求图中阴影部分的面积.24. 近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A,B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和3台B种设备需要5.5万元.(1)、求每台A种、B种设备各多少万元?(2)、根据学校实际,需购进A种和B种设备共40台,总费用不超过40万元,请你通过计算,求至少购买A种设备多少台?
(1)、求证:AC是⊙O的切线;(2)、若AB=OC=8,求图中阴影部分的面积.24. 近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A,B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和3台B种设备需要5.5万元.(1)、求每台A种、B种设备各多少万元?(2)、根据学校实际,需购进A种和B种设备共40台,总费用不超过40万元,请你通过计算,求至少购买A种设备多少台?

